题目内容
14. 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.(1)求抛物线解析式;
(2)求证:△BCD为直角三角形;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
分析 (1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(-1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而求得a=-1,b=2;
(2)先利用配方法求出抛物线的顶点D的坐标,再利用两点间的距离公式得出CD2+BC2=BD2,由勾股定理的逆定理即可证明△BCD为直角三角形;
(3)由(2)知,CD=$\sqrt{2}$,BC=$\sqrt{18}$=3$\sqrt{2}$.设M(x,-x2+2x+3),则MN=-x2+2x+3,BN=3-x,由于∠MNB=∠BCD=90°,所以当△BMN与△BCD相似时,分两种情况:①△BMN∽△BDC;②△BMN∽△DBC.然后根据相似三角形的性质列出关于x的方程,从而求得点M的坐标.
解答 解:(1)∵将x=0代入y=ax2+bx+3,得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1,
∴A(-1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(-1,0),B(3,0)代入y=ax2+bx+3得:
$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$.
∴抛物线解析式为y=-x2+2x+3; (2)∵y=-x2+2x+3=-(x-1)2+4,
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4).
∵A(-1,0),B(3,0),C(0,3),
∴CD2=(1-0)2+(4-3)2=2,
BC2=(3-0)2+(0-3)2=18,
BD2=(1-3)2+(4-0)2=20,
∴CD2+BC2=BD2,
∴△BCD为直角三角形;
(3)由(2)知,CD=$\sqrt{2}$,BC=$\sqrt{18}$=3$\sqrt{2}$.
设在x轴上方的抛物线上存在点M(x,-x2+2x+3),则-1<x<3,-x2+2x+3>0,
∵MN⊥x轴于N点,
∴N(x,0),∠MNB=90°,
∴BN=3-x,MN=-x2+2x+3.
∵Rt△BCD中,∠BCD=90°,
∴∠MNB=∠BCD=90°,
∴当△BMN与△BCD相似时,分两种情况:
①如果△BMN∽△BDC,那么$\frac{MN}{CD}$=$\frac{BN}{BC}$,
即$\frac{-{x}^{2}+2x+3}{\sqrt{2}}$=$\frac{3-x}{3\sqrt{2}}$,
解得x1=3,x2=-$\frac{2}{3}$,
又∵-1<x<3,
∴x=-$\frac{2}{3}$,
∴-x2+2x+3=$\frac{11}{9}$,
∴M(-$\frac{2}{3}$,$\frac{11}{9}$);
②如果△BMN∽△DBC,那么$\frac{MN}{BC}$=$\frac{BN}{CD}$,
即$\frac{-{x}^{2}+2x+3}{3\sqrt{2}}$=$\frac{3-x}{\sqrt{2}}$,
解得x1=2,x2=3,
又∵-1<x<3,
∴x=2,
∴-x2+2x+3=3,
∴M(2,3).
综上所述,M点坐标为(-$\frac{2}{3}$,$\frac{11}{9}$)或(2,3).
点评 本题是二次函数综合题,其中涉及到利用待定系数法求二次函数的解析式、二次函数的性质、两点间的距离公式、勾股定理的逆定理、相似三角形的性质等知识点,利用分类讨论、数形结合与方程思想是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 0cm | B. | 3cm | C. | 6cm | D. | 9cm |
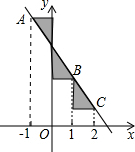 如图,点A、B、C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
如图,点A、B、C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )| A. | 3(m-1) | B. | $\frac{3}{2}(m-2)$ | C. | 1 | D. | 3 |
 某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为一商场提供家电配件,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为100元,生产每件配件的人力成本为5元,其它成本3元,该配件在1至9月的销售量p1(万件)与月份x满足函数关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)与月份x满足函数关系式p2=-0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1月份,每件配件的原材料价格均比去年10月上涨8元,人力成本比去年增加1元,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少8a%.这样,该月完成了17万元利润的任务,请你计算出a的值.
| A. | k>-$\frac{1}{3}$ | B. | k>$\frac{1}{3}$ | C. | k<-$\frac{1}{3}$ | D. | k<$\frac{1}{3}$ |
 如表是我国某城市A区和B区2013年5月至12月的月平均商品住房成交数(单位:套)统计表:
如表是我国某城市A区和B区2013年5月至12月的月平均商品住房成交数(单位:套)统计表:| 月份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A区 | 320 | 315 | 325 | 310 | 315 | 305 | 340 | 315 |
| B区 | 330 | 325 | 315 | 345 | 320 | 315 | 310 | 335 |
(2)A,B两区月平均商品住房成交数差别最大的月份是8月,月平均商品住房成交数差别最小的月份是9月.
 如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象没有公共点,则b的取值范围是-2<b<2.
如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象没有公共点,则b的取值范围是-2<b<2.