Question

18．如图，锐角三角形ABC中，BC=6，BC边上的高线长为4，PQRS是△ABC的内接矩形，且S_矩形PQRS=$\frac{1}{4}$S_△ABC，记$\frac{BS}{BA}$=λ，求λ的值．

Answer 1

分析 可由△ASR∽△ABC得出对应边成比例，再由三角形与梯形的面积比建立等式，即可得出结论．

解答 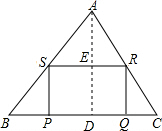证明：如图，过A作AD⊥BC于D，交SR于E，
∵SR∥BC，
∴AE⊥SR，
设PS=x，RS=y，
∵SR∥BC，
∴△ASR∽△ABC，得$\frac{4-x}{4}=\frac{y}{6}$，
∴y=6-$\frac{3x}{2}$，
∵S_矩形PQRS=$\frac{1}{4}$S_△ABC，即x（6-$\frac{3x}{2}$）=$\frac{1}{4}×\frac{1}{2}$×6×4，
∴x=2+$\sqrt{2}$，或x=2-$\sqrt{2}$，
∴DE=PS=2+$\sqrt{2}$，或DE=PS=2-$\sqrt{2}$，
∵SR∥BC，∴$\frac{BS}{BA}$=$\frac{DE}{AD}$=λ，
∴λ=$\frac{2+\sqrt{2}}{4}$或λ$\frac{2-\sqrt{2}}{4}$．

点评 本题主要考查了相似三角形的判定及性质以及一元二次方程的求解问题，能够熟练掌握．