题目内容
1．
如图，DE∥BC，若AD=4，DB=6，BC=12，则DE的长为$\frac{24}{5}$．
分析 由DE∥BC，可得△ADE∽△ABC，然后由相似三角形的对应边成比例，求得答案．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，
∵AD=4，DB=6，BC=12，
∴AB=AD+DB=10，
∴$\frac{4}{10}$=$\frac{DE}{12}$，
解得：DE=$\frac{24}{5}$．
故答案为：$\frac{24}{5}$．
点评 此题考查了相似三角形的判定与性质．注意证得△ADE∽△ABC是解此题的关键．
练习册系列答案
相关题目
如图，△ABC中，D、E分别为AB、AC上的点，BE、CD相交于点G，若G为△ABC的重心，则DE：BC=1：2，△BDG的面积：△BEC的面积=1：3．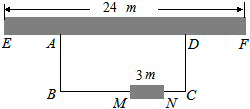
如图，利用一面墙（墙EF最长可利用24米），围成一个矩形花园ABCD，与围墙平行的一边BC上要预留3米宽的入口（如图MN所示，不用砌墙），用46米长的墙的材料做围墙，设这个苗圃园垂直于墙的一边的长为x米．