题目内容
9.在同一直角坐标系中,一次函数y=-x+2与y=2x+2的图象与x轴围成的三角形的面积是3,周长是$\sqrt{5}$+2$\sqrt{2}$+3.分析 作出两个函数的图象,求出图象与坐标轴的交点以及两个函数图象的交点.进而可求出三角形的面积与周长.
解答 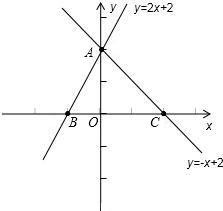 解:如图:直线y=2x+2与x轴的交点为B(-1,0),
解:如图:直线y=2x+2与x轴的交点为B(-1,0),
直线y=-x+2与x轴的交点为C(2,0);
两个函数的交点是A(0,2);
∴BC=3,AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{5}$,AC=2$\sqrt{2}$;
则S△ABC=$\frac{1}{2}$BC•OA=3;C△ABC=$\sqrt{5}$+2$\sqrt{2}$+3
故答案为3;$\sqrt{5}$+2$\sqrt{2}$+3.
点评 本题考查了一次函数图象上点的特征,三角形的面积与周长,求得交点坐标是解题关键.

练习册系列答案
相关题目
18.若m+n=0,则m,n的取值一定是( )
| A. | 都是0 | B. | 至少有一个等于0 | C. | 互为相反数 | D. | m是正数,n是负数 |
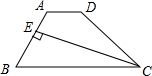 如图,在四边形ABCD中,AD∥BC,若∠BCD的平分线CE⊥AB于点E,BE=2AE,且四边形AECD的面积为21,则△EBC的面积=24.
如图,在四边形ABCD中,AD∥BC,若∠BCD的平分线CE⊥AB于点E,BE=2AE,且四边形AECD的面积为21,则△EBC的面积=24.
 如图,DE∥BC,若AD=4,DB=6,BC=12,则DE的长为$\frac{24}{5}$.
如图,DE∥BC,若AD=4,DB=6,BC=12,则DE的长为$\frac{24}{5}$.