题目内容
3.已知相交两圆的半径分别为15和20,公共弦的长为24,求这两圆的圆心距.分析 先根据勾股定理,可得得圆心距的两部分分别是9,16,然后根据两圆的位置关系确定圆心距.
解答 解:如图1,AB=24,O1A=15,O2A=20,
∵公共弦长为24,
∴AC=12,AB⊥O1O2,
∴O1C=$\sqrt{{O}_{1}{A}^{2}-A{C}^{2}}$=9,O2C=$\sqrt{{O}_{2}{A}^{2}-A{C}^{2}}$=16,
∴①当公共弦在两个圆心之间时,圆心距=9+16=25;
②当公共弦在圆心的同侧时,如图2,圆心距=16-9=7;
故这两个圆的圆心距是25或7.
点评 此题综合考查了相交两圆的性质以及勾股定理.注意此题应考虑两种情况.

练习册系列答案
相关题目
12.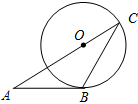 如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )
如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )
 如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )
如图,AB与⊙O目切于点B,连接AO,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为( )| A. | 50° | B. | 25° | C. | 20° | D. | 15° |
11.在函数y=$\frac{{\sqrt{x-3}}}{x-3}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x≠-3 | D. | x>-3且x≠0 |
8.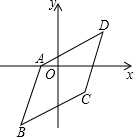 如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
 如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )| A. | (3,1) | B. | (3,2) | C. | (3,3) | D. | (3,4) |
13.估算$\sqrt{63}$-$\sqrt{7}$的值在( )
| A. | 3和4之间 | B. | 4和5之间 | C. | 5和6之间 | D. | 6和7之间 |

 如图,下面的几何体由两个大小相同的正方体和一个圆柱体组成,则它的左视图是( )
如图,下面的几何体由两个大小相同的正方体和一个圆柱体组成,则它的左视图是( )


