题目内容
8.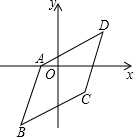 如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )
如图,已知?ABCD三个顶点坐标是A(-1,0)、B(-2,-3)、C(2,-1),那么第四个顶点D的坐标是( )| A. | (3,1) | B. | (3,2) | C. | (3,3) | D. | (3,4) |
分析 过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,求出△DCN≌△BAE,根据全等三角形的性质得出BE=DN,AE=CN,根据A、B、C的作求出OM和DM即可.
解答 解:
过B作BE⊥x轴于E,过D作DM⊥x轴于M,过C作CF⊥BE于F,DM和CF交于N,
则四边形EFNM是矩形,
所以EF=MN,EM=FN,FN∥EM,
∴∠EAB=∠AQC,
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠AQC=∠DCN,
∴∠DCN=∠EAB,
在△DCN和△BAE中
$\left\{\begin{array}{l}{∠N=∠BEA=90°}\\{∠DCN=∠EAB}\\{CD=AB}\end{array}\right.$
∴△DCN≌△BAE,
∴BE=DN,AE=CN,
∵A(-1,0)、B(-2,-3)、C(2,-1),
∴CN=AE=2-1=1,DN=BE=3,
∴DM=3-1=2,OM=2+1=3,
∴D的坐标为(3,2),
故选B.
点评 本题考查了全等三角形的性质和判定,平行四边形的性质,点的坐标与图形性质等知识点,能正确作出辅助线是解此题的关键.

练习册系列答案
相关题目
17. 如图,正方形ABCD中,BP=PQ=QC,AQ与DP交于R,若正方形ABCD的面积为100cm2,则△PQR的面积为 ( )cm2.
如图,正方形ABCD中,BP=PQ=QC,AQ与DP交于R,若正方形ABCD的面积为100cm2,则△PQR的面积为 ( )cm2.
 如图,正方形ABCD中,BP=PQ=QC,AQ与DP交于R,若正方形ABCD的面积为100cm2,则△PQR的面积为 ( )cm2.
如图,正方形ABCD中,BP=PQ=QC,AQ与DP交于R,若正方形ABCD的面积为100cm2,则△PQR的面积为 ( )cm2.| A. | 25 | B. | $\frac{50}{3}$ | C. | $\frac{25}{12}$ | D. | $\frac{25}{6}$ |
19.一个数a在数轴上的对应点在原点的左边,且|a|=4,则a的值为( )
| A. | 4或-4 | B. | 4 | C. | -4 | D. | 以上都不对 |
20.下列因式分解中正确的是( )
| A. | m2-n2=(m-n)2 | B. | 3m2-6m-9=3(m-3)(m+1) | ||
| C. | x4-2x2y2+y4=(x2-y2)2 | D. | x2-3x-4=(x+4)(x-1) |
17.下列句子中不是命题的是( )
| A. | 两直线平行,同位角相等 | B. | 直线AB和直线CD不一定垂直 | ||
| C. | 若|a|=|b|,则a2=b2 | D. | 同角的补角相等 |
18.由以下三边不能组成直角三角形的是( )
| A. | 5,13,12 | B. | 2,3,$\sqrt{5}$ | C. | 4,7,5 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
 如图所示,∠AOE=90°,∠BOD=45°,那么不大于90°的所有角的度数之和是450度.
如图所示,∠AOE=90°,∠BOD=45°,那么不大于90°的所有角的度数之和是450度. 如图,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动.当△PQC为等腰三角形时,则t的值为2.
如图,在 Rt△ABC中,∠ACB=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动.当△PQC为等腰三角形时,则t的值为2.