题目内容
13.估算$\sqrt{63}$-$\sqrt{7}$的值在( )| A. | 3和4之间 | B. | 4和5之间 | C. | 5和6之间 | D. | 6和7之间 |
分析 首先化简二次根式,进而利用二次根式的性质估算得出答案.
解答 解:∵$\sqrt{63}$=3$\sqrt{7}$,
∴$\sqrt{63}$-$\sqrt{7}$=3$\sqrt{7}$-$\sqrt{7}$=2$\sqrt{7}$,
∵2$\sqrt{7}$=$\sqrt{28}$,
∴5<$\sqrt{28}$<6,
∴$\sqrt{63}$-$\sqrt{7}$的值在:5和6之间,
故选:C.
点评 此题主要考查了估算无理数的大小,正确化简二次根式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在下列给出的条件中,能判定四边形ABCD是平行四边形的是( )
| A. | ∠A=∠B,∠C=∠D | B. | AB∥CD,AD=BC | C. | AB=BC,AD=DC | D. | AB∥CD,∠B=∠D |
8.如果a=-3-2,b=-0.32,c=(-$\frac{1}{3}$)-2,d=(-$\frac{1}{5}$)0,那么a,b,c,d三数的大小为( )
| A. | a<b<c<d | B. | b<a<d<c | C. | a<d<c<b | D. | a<b<d<c |
18.由以下三边不能组成直角三角形的是( )
| A. | 5,13,12 | B. | 2,3,$\sqrt{5}$ | C. | 4,7,5 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
5.已知:a=(-99)0,b=(-0.1)-1,c=(-$\frac{5}{3}$)-2,那么a,b,c三数的大小为( )
| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | a<c<b |
3. 如图所示,已知在△ABC中,AD是高,若∠C=40°,则∠DAC的度数为( )
如图所示,已知在△ABC中,AD是高,若∠C=40°,则∠DAC的度数为( )
 如图所示,已知在△ABC中,AD是高,若∠C=40°,则∠DAC的度数为( )
如图所示,已知在△ABC中,AD是高,若∠C=40°,则∠DAC的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
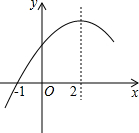 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④若点A(-3,y1),点B(-12,y2),点C(72,y3)在该函数图象上,则y1<y3<y2;⑤若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④若点A(-3,y1),点B(-12,y2),点C(72,y3)在该函数图象上,则y1<y3<y2;⑤若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )