题目内容
12.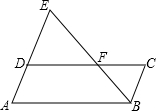 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B. | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D. | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
分析 由四边形ABCD是平行四边形,可得CD∥AB,AD∥BC,CD=AB,AD=BC,然后平行线分线段成比例定理,对各项进行分析即可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC,CD=AB,AD=BC,
∴$\frac{ED}{EA}$=$\frac{DF}{AB}$,故A正确,选项不符合题意;
∴$\frac{DE}{CB}$=$\frac{EF}{FB}$正确,B选项不符合题意;
$\frac{BF}{BE}$=$\frac{BC}{AE}$,正确,故C不符合题意;
∴$\frac{BC}{DE}$=$\frac{BF}{BE}$,错误,D符合题意.
故选D.
点评 本题考查平行线分线段成比例定理,找准对应关系,避免错选其他答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知a,b,c满足$\frac{a}{2}$=$\frac{b-c}{3}$=$\frac{a+c}{5}$,则$\frac{a+c}{2a+b}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
20.将一副直角三角板如图放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合,则α的值为( )
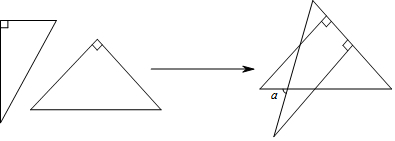

| A. | 30° | B. | 45° | C. | 70° | D. | 75° |
4.以下说法正确的是( )
| A. | 有理数与数轴上的点一一对应 | |
| B. | 两个无理数的积一定是无理数 | |
| C. | 负数没有平方根也没有立方根 | |
| D. | 算术平方根等于它本身的数只有0或1 |
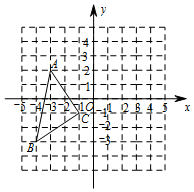 如图,(1)画出△ABC先向右平移4个单位,再向上平移1个单位后的图形△A'B'C';
如图,(1)画出△ABC先向右平移4个单位,再向上平移1个单位后的图形△A'B'C';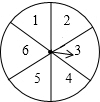 转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解:
转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解: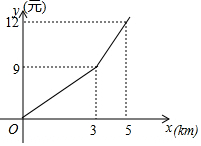 某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.
某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.