题目内容
3．解分式方程：$\frac{x}{x+2}$-1=$\frac{2}{x}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：两边同乘x（x+2）得：x2-x2-2x=2x+4，
解得：x=-1，
经检验x=-1是分式方程的解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
相关题目
某学校要了解学生上学交通情况，选取七年级全体学生进行调查，根据调查结果，画出扇形统计图（如图），图中“公交车”对应的扇形圆心角为60°，“自行车”对应的扇形圆心角为120°，已知七年级乘公交车上学的人数为50人．
14．下列各数中，最大的数是（ ）
| A． | -$\frac{1}{2}$ | B． | （-$\frac{1}{2}$）2 | C． | （-$\frac{1}{2}$）3 | D． | （-$\frac{1}{2}$）4 |
如图，∠MON=30°，且OP平分∠MON，过点P作PQ∥OM交ON于点Q．若点P到OM的距离为2，则OQ的长为（ ）
8．下面的说法正确的是（ ）
| A． | -2不是单项式 | B． | -a表示负数 | C． | $\frac{3ab}{5}$的系数是3 | D． | x2+2x+1是多项式 |
从正面和左面看到长方体的图形如图所示（单位：cm），则从其上面看到图形的面积是12cm2．
12．
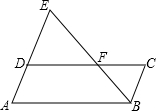如图，点F是?ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（ ）
如图，点F是?ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（ ）| A． | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B． | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C． | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D． | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
