题目内容
20.将一副直角三角板如图放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合,则α的值为( )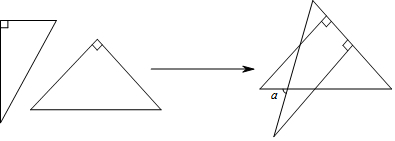
| A. | 30° | B. | 45° | C. | 70° | D. | 75° |
分析 根据三角形的内角和求出∠2=45°,再根据对顶角相等求出∠3=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可.
解答  解:∵∠2=90°-45°=45°(直角三角形两锐角互余),
解:∵∠2=90°-45°=45°(直角三角形两锐角互余),
∴∠3=∠2=45°,
∴∠α=∠3+30°=45°+30°=75°.
故选D.
点评 本题考查的是三角形的内角和,三角形外角的性质,熟知三角形的一个外角等于与它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下面的说法正确的是( )
| A. | -2不是单项式 | B. | -a表示负数 | C. | $\frac{3ab}{5}$的系数是3 | D. | x2+2x+1是多项式 |
12.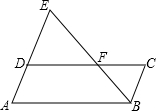 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
 如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是?ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B. | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D. | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
 如图,C是线段AB的中点,点D在CB上,且AD=6.5,BD=1.5,则线段CD长为2.5.
如图,C是线段AB的中点,点D在CB上,且AD=6.5,BD=1.5,则线段CD长为2.5. 从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是12cm2.
从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是12cm2. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为55°.
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为55°. 等腰△ABC、△EFC中,AB=AC,FE=FC,D为BE的中点,∠BAC+∠EFC=180°,求证:AD⊥FD.
等腰△ABC、△EFC中,AB=AC,FE=FC,D为BE的中点,∠BAC+∠EFC=180°,求证:AD⊥FD.