题目内容
6. 在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-$\frac{1}{3}$,-$\frac{1}{3}$),(-$\sqrt{2}$,-$\sqrt{2}$),…,都是和谐点.
在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-$\frac{1}{3}$,-$\frac{1}{3}$),(-$\sqrt{2}$,-$\sqrt{2}$),…,都是和谐点.(1)分别判断函数y=-2x+1和y=x2+1的图象上是否存在和谐点,若存在,求出其和谐点的坐标;
(2)若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点($\frac{3}{2}$,$\frac{3}{2}$),且当0≤x≤m时,函数y=ax2+4x+c-$\frac{3}{4}$(a≠0)的最小值为-3,最大值为1,求m的取值范围.
(3)直线l:y=kx+2经过和谐点P,与x轴交于点D,与反比例函数G:y=$\frac{n}{x}$的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且DM+DN<3$\sqrt{2}$,请直接写出n的取值范围.
分析 (1)根据和谐点的横坐标与纵坐标相同,可得关于a的方程,根据解方程,可得答案.
(2)根据和谐点的概念令ax2+4x+c=x,即ax2+3x+c=0,由题意,△=32-4ac=0,即4ac=9,方程的根为$\frac{-3}{2a}=\frac{3}{2}$,从而求得a=-1,$c=-\frac{9}{4}$,所以函数y=ax2+4x+c-$\frac{3}{4}$=-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
(3)根据题意得出当n>0时,以及当n<0时,分别利用数形结合得出n的取值.
解答 解:(1)存在,
令-2x+1=x,解得$x=\frac{1}{3}$,
∴函数y=-2x+1的图象上有一个和谐点($\frac{1}{3}$,$\frac{1}{3}$);
令x2+1=x,即x2-x+1=0,
∵根的判别式△=(-1)2-4×1×1=-3<0,
∴方程x2-x+1=0无实数根,
∴函数y=x2+1的图象上不存在和谐点.
(2)令ax2+4x+c=x,即ax2+3x+c=0,
由题意,△=32-4ac=0,即4ac=9,
又方程的根为$\frac{-3}{2a}=\frac{3}{2}$,
解得a=-1,$c=-\frac{9}{4}$.
故函数$y=a{x^2}+4x+c-\frac{3}{4}$,即y=-x2+4x-3,
如图1,该函数图象顶点为(2,1),与y轴交点为(0,-3),由对称性,该函数图象也经过点(4,-3). 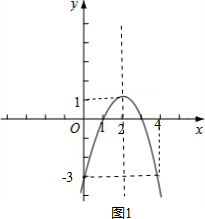
由于函数图象在对称轴x=2左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小,且当0≤x≤m时,函数y=-x2+4x-3的最小值为-3,最大值为1,
∴2≤m≤4.
(3)$-\frac{5}{4}<n<0$,或0<n<1.
∵y=kx+2经过和谐点P,
∴y=x,
∴x=kx+2,
∴点P的横坐标为1,
∴k=-1,
∴直线l为:y=-x+2,
分两种情况: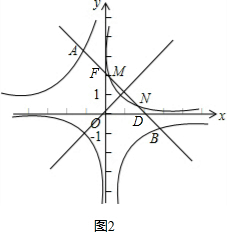
①如图2,当n>0时,
∵y=-x+2,与x轴交于点D(2,0),与y轴交于点F(0,2),
∴DF=2$\sqrt{2}$,
∴DM+DN<3$\sqrt{2}$,
∴只要y=-x+2与y=$\frac{n}{x}$有交点坐标即可,
∴-x+2=$\frac{n}{x}$,
整理得:x2-2x+n=0,
∴b2-4ac>0,
∴4-4n>0,
解得:n<1,
则0<n<1;
②如图3,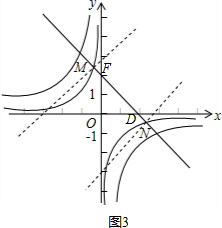
当n<0时,当DM+DN=3$\sqrt{2}$,
则DN=FM=$\frac{\sqrt{2}}{2}$,
∵y=-x+2,与x轴交于点D(2,0),与y轴交于点F(0,2),
∴可求出M(-$\frac{1}{2}$,$\frac{5}{2}$),
则xy=n=-$\frac{5}{4}$,
则-$\frac{5}{4}$<n<0.
综上,当-$\frac{5}{4}$<n<0或0<n<1时,反比例函数G2的图象与直线l有两个公共点M,N,且DM+DN<3$\sqrt{2}$.
点评 本题是二次函数的综合题,考查了二次函数图象上点的坐标特征,二次函数的性质以及根的判别式等知识,利用分类讨论以及数形结合得出是解题关键.

| A. | m≤2或m≥3 | B. | m≤3或m≥4 | C. | 2<m<3 | D. | 3<m<4 |

 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积. 如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于O点,求证:BE=CD.
如图,在等腰△ABC中,AB=AC,两底角的平分线BE和CD相交于O点,求证:BE=CD.