题目内容
13. 如图:在△ABC中,AB=7,AC=5,AD是它的角平分线,则S△ABD:S△ACD=$\frac{7}{5}$.
如图:在△ABC中,AB=7,AC=5,AD是它的角平分线,则S△ABD:S△ACD=$\frac{7}{5}$.
分析 根据角平分线的性质求出$\frac{BD}{CD}$,根据等高的两个三角形的面积比等于对应的底的比计算即可.
解答 解:∵AD是△ABC的角平分线,AB=7,AC=5,
∴$\frac{BD}{CD}$=$\frac{AB}{AC}$=$\frac{7}{5}$,
∴S△ABD:S△ACD=$\frac{7}{5}$,
故答案为:$\frac{7}{5}$.
点评 本题考查的是角平分线的性质和三角形的面积的计算,掌握等高的两个三角形的面积比等于对应的底的比是解题的关键.

练习册系列答案
相关题目
4. 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=( )| A. | 195° | B. | 250° | C. | 270° | D. | 无法确定 |
18.已知点E在如图1的长方形纸带AD上,作∠DEF=α,将纸带沿EF折叠成图2,再沿BF折叠成图3中的∠CFE=114°,那么α的大小为( )
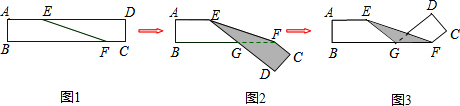

| A. | 27° | B. | 26° | C. | 23° | D. | 22° |
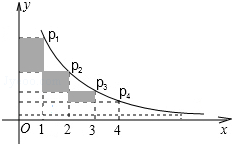 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,…,P2010,它们的横坐标依次为1,2,3,…,2015.分别过这些点作 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).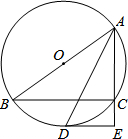 如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.
如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.