题目内容
已知：如图，平行四边形ABCD中，∠ADC的平分线与AB相交于点E．求证：BE+BC=CD．考点：平行四边形的性质
专题：证明题
分析：根据平行四边形的性质得出AD=BC，CD=AB，DC∥AB，求出∠ADE=∠DEA=∠CDE，推出AD=AE=BC，即可得出答案．
解答：证明：∵四边形ABCD是平行四边形，
∴AD=BC，CD=AB，DC∥AB，
∴∠CDE=∠DEA，
∵DE平分∠ADC，
∴∠CDE=∠ADE，
∴∠ADE=∠DEA，
∴AD=AE=BC，
∵ABE=AB，
∴BE+BC=CD．
∴AD=BC，CD=AB，DC∥AB，
∴∠CDE=∠DEA，
∵DE平分∠ADC，
∴∠CDE=∠ADE，
∴∠ADE=∠DEA，
∴AD=AE=BC，
∵ABE=AB，
∴BE+BC=CD．
点评：本题考查了平行四边形的性质，平行线的性质，等腰三角形的判定的应用，主要考查学生的推理能力．
练习册系列答案
名校课堂系列答案
相关题目
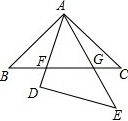如图所示，已知△ABC和△DAE都是等腰直角三角形，∠BAC=∠ADE=90°，BC与AD、AE分别交于点F、G．图中哪些三角形相似？说明理由．一个正多边形，它的一个外角等于与它相邻的内角的
，则这个多边形是（ ）
| 1 |
| 4 |
| A、正十二边形 | B、正十边形 |
| C、正八边形 | D、正六边形 |