题目内容
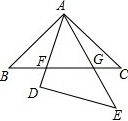 如图所示,已知△ABC和△DAE都是等腰直角三角形,∠BAC=∠ADE=90°,BC与AD、AE分别交于点F、G.图中哪些三角形相似?说明理由.
如图所示,已知△ABC和△DAE都是等腰直角三角形,∠BAC=∠ADE=90°,BC与AD、AE分别交于点F、G.图中哪些三角形相似?说明理由.考点:相似三角形的判定
专题:
分析:因为△ABC与△ADE是全等的等腰三角形,所以可得:∠B=∠C=∠E=∠EAD=45°,在△ABF与△GAF中∠AFB是公共角,在△AGC与△CGA中∠AGF是公共角,根据相似三角形的判定定理:有两个角分别对应相等的三角形相似,可得△ABF∽△GAF,△GCA∽△GAF;再根据相似三角形的传递性,可得△ABF∽△GCA.
解答:解:依题意可知,△ABF∽△GAF,△GCA∽△GAF;再根据相似三角形的传递性,可得△ABF∽△GCA;
理由如下:∵△ABC与△ADE是全等的等腰直角三角形,
∴∠B=∠C=∠E=∠EAD=45°,
∵∠AFB=∠AFG,∠AGF=∠BAF,
∴△ABF∽△GAF,△GCA∽△GAF,
∴△ABF∽△GCA.
理由如下:∵△ABC与△ADE是全等的等腰直角三角形,
∴∠B=∠C=∠E=∠EAD=45°,
∵∠AFB=∠AFG,∠AGF=∠BAF,
∴△ABF∽△GAF,△GCA∽△GAF,
∴△ABF∽△GCA.
点评:此题考查了相似三角形的判定(有两个角分别对应相等的三角形相似).解此题的关键是要注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图. 已知:如图,平行四边形ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
已知:如图,平行四边形ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD. 如图,在△ABC中,AD是边BC上的高,BC=AD=12,sinB=
如图,在△ABC中,AD是边BC上的高,BC=AD=12,sinB=