题目内容
14．若二次函数y=ax2+b的图象经过点P（-2，4），则下列各点中，一定在该图象上的是（ ）| A． | （-4，2） | B． | （4，-2） | C． | （2，4） | D． | （-2，-4） |
分析 把x=-2，y=4代入y=ax2+b，得出关于a，b的关系，再代入即可判断．
解答 解：把x=-2，y=4代入y=ax2+b，
可得：4=4a+b，
A、把x=-4，y=2代入y=ax2+b，可得：2=16a+b，不符合题意；
B、把x=4，y=-2代入y=ax2+b，可得：-2=16a+b，不符合题意；
C、把x=2，y=4代入y=ax2+b，可得：4=4a+b，符合题意；
D、把x=-2，y=-4代入y=ax2+b，可得：-4=4a+b，不符合题意；
故选C
点评 本题考查了二次函数图象上点的坐标特征：图象上的点的坐标代入解析式成立．
练习册系列答案
相关题目
4．
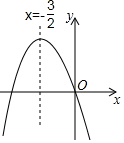如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0；②a+b+c＞0；③a＞b；④b2-4ac＜0；其中正确的结论有（ ）
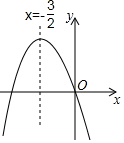如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0；②a+b+c＞0；③a＞b；④b2-4ac＜0；其中正确的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．圆内接四边形ABCD中，已知∠A=70°，则∠C等于（ ）
| A． | 110° | B． | 70° | C． | 30° | D． | 20° |
9．已知⊙O的半径为1，圆心O的坐标为（0，0），点P的坐标为（$\sqrt{2}$，-1），则点P与⊙O的位置关系是（ ）
| A． | 点P在⊙O内 | B． | 点P在⊙O上 | C． | 点P在⊙O外 | D． | 点P在⊙O上或⊙O外 |
