题目内容
20.如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.(1)直尺的长为20个单位长度(直接写答案)
(2)如图2,直尺AB在数轴上移动,有BC=4OA,求此时A点对应的数;
(3)如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2,若t1-t2=2(秒),求直尺放入蓬内,A点对应的数为多少?

分析 (1)由题可知:OA=AB=BC,所以60÷3=20,则AB=20;
(2)有两种情况:利用图形直观得出,根据等量关系式BC=4OA,列式可求解;
(3)设A点对应的数为a(a>0),向左移动所用的时间t1=$\frac{20+a}{5}$,向右移动所用的时间t2=$\frac{60-a}{5}$,根据t1-t2=2列式计算即可.
解答 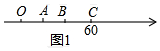 解:(1)如图1,由题意得:OA=AB=BC,
解:(1)如图1,由题意得:OA=AB=BC,
∵OC=60,
∴AB=20,
故答案为:20;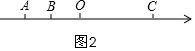
(2)由题意可知:直尺一定在C的左侧,
当AB在O的右侧时,如图2,
设点A表示的数为x(x<0),
∵BC=4OA,
∴60-x-20=-4x,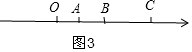
x=-$\frac{40}{3}$,
当AB在线段OC上时,如图3,
设点A表示的数为x(x>0),则OA=x,BC=60-20-x,
由BC=4OA得:60-20-x=4x,
x=8,
综上所述,A点对应的数是-$\frac{40}{3}$或8;
(3)设A点对应的数为a(a>0),
则$\frac{a+20}{5}-\frac{60-a}{5}$=2,
解得a=25,
答:A点对应的数为25.
点评 本题是数轴问题,与平移变换相结合,考查了数轴上表示的有理数与线段的长之间的关系;若点A表示的数为xA,点B表示的数为xB,则AB=|xA-xB|.

练习册系列答案
相关题目
12.若方程x2+ax-2a-3=0有两个相等的实数根,则a的值是( )
| A. | 2或6 | B. | -2或-6 | C. | $\frac{18}{5}$ | D. | 3或4 |