题目内容
20．（1）解方程：x2-2x-8=0．（2）用配方法解方程：x2+4x+2=0．
分析 （1）利用十字相乘法分解因式解方程即可；
（2）直接利用配方法解方程得出答案．
解答 解：（1）（x+2）（x-4）=0，
则x+2=0或x-4=0，
解得：x1=-2，x2=4；
（2）x2+4x=-2，
x2+4x+4=2，
（x+2）2=2，
x+2=±$\sqrt{2}$，
解得：x1=-2+$\sqrt{2}$，x2=-2-$\sqrt{2}$．
点评 此题主要考查了因式分解法、配方法解方程，正确分解因式是解题关键．
练习册系列答案
相关题目
10．已知：四边形ABCD是正方形，在平面内找一点P满足△PAB，△PBC，△PCD，△PAD均为等腰三角形，这样的点P有（ ）个．
| A． | 7个 | B． | 8个 | C． | 9个 | D． | 10个 |
8．方程x2-4x-4=0进行配方后，得到的方程是（ ）
| A． | （x-2）2=8 | B． | （x+2）2=8 | C． | （x-2）2=0 | D． | （x+2）2=16 |
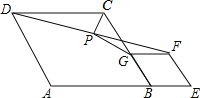如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC=∠BEF=60°，则$\frac{CP}{CG}$=$\frac{1}{2}$．
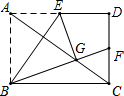如图，在矩形ABCD中，点E为AD的中点，将△ABE沿BE折叠后得到△GBE，点G恰好在矩形ABCD的对角线AC上，延长BG交CD于F，连接EF．求$\frac{BE}{EF}$的值．
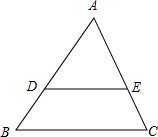如图，$\frac{AD}{DB}$=$\frac{AE}{EC}$=2，求$\frac{AB}{DB}$、$\frac{AE}{AC}$的值．