题目内容
11.在△ABC中,AB=AC,D在AC上,AE=AC交BD的延长线于点E,AF平分∠CAE交BE于F(1)如图1,连CF,求证:∠ABE=∠ACF;
(2)如图2,当∠ABC=60°时,请写出AF、EF、BF的数量关系,不需证明;
(3)如图3,若∠BAC=90°,且BD平分∠ABC,求证:BD=2EF.
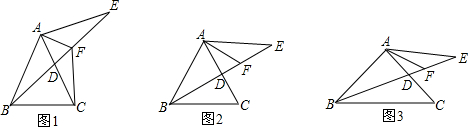
分析 (1)由于AB=AE,因此只需证△FAE≌△FAC即可;
(2)在BF上截取BG=EF,再证AF=GF即可,也就是证三角形AFG是等边三角形即可,由所给条件结合(1)中结论可知AF=CF=EF,结论显然;
(3)由(1)中结论可知∠ABE=∠ACF,从而马上可得∠BFC=90°,延长CF交BA于点H,则由三线合一可知CH=2CF=2EF,因此只需证BD=CH即可,也就只需证△ABD与△ACH全等,结论显然.
解答 解:(1)∵AB=AC,AE=AC,
∴AB=AE,
∴∠ABE=∠AEB,
∵AF平分∠CAE交BE于F,
∴∠FAE=∠FAC,
在△FAE和△FAC中,
$\left\{\begin{array}{l}{FA=FA}\\{∠FAE=∠FAC}\\{AE=AC}\end{array}\right.$,
∴△FAE≌△FAC(SAS),
∴∠ACF=∠AEF=∠ABE;
(2)在BD上截取BG=EF,连接CF,如图2,
在△ABG和△AEF中,
$\left\{\begin{array}{l}{BA=EA}\\{∠ABG=∠AEG}\\{BG=EF}\end{array}\right.$,
∴△ABG≌△AEF(SAS),
∴AG=AF,
∵BA=BC,BD平分∠ABC,
∴BD垂直平分AC,∠ABG=∠AEF=30°
∴FA=FC,
∵FC=FE,
∴AF=EF,
∴AG=BG,
∴∠AGF=∠AFG=60°,
∴△AGF是等边三角形,
∴AG=GF=AF,
BF=BG+GF=AF+EF;
(3)连接CF并延长交BA于点H,如图3,
∵∠ABD=∠ACF,∠BAD=90°,
∴∠CFD=90°,
∵BD平分∠ABC,
∴CF=FH,
在△ABD和△ACH中,
$\left\{\begin{array}{l}{∠BAD=∠CAH}\\{AB=AC}\\{∠ABD=∠ACH}\end{array}\right.$,
∴△ABD≌△ACH(ASA),
∴BD=CH=2CF=2EF.
点评 本题考查了等腰三角形的性质、角平分线的性质、全等三角形的判定与性质、等边三角形的判定与性质等知识点,难度中等.解答本题的关键在于识别和构造全等三角形并寻找全等的条件,注意三线合一等常见结论的应用.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | $\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
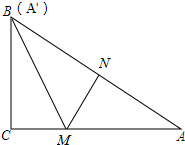 如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.
如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.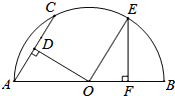 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为1.
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为1.