题目内容
10．已知：四边形ABCD是正方形，在平面内找一点P满足△PAB，△PBC，△PCD，△PAD均为等腰三角形，这样的点P有（ ）个．| A． | 7个 | B． | 8个 | C． | 9个 | D． | 10个 |
分析 根据题意得出有三种情况：①正方形对角线交点，②画出图形，结合图形得出结论，③和②类似得出符合条件的四个点，即可得出答案．
解答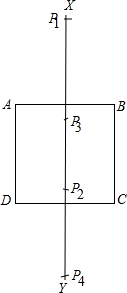 
解：分为三种情况：①正方形对角线的交点；
②作AB的垂直平分线XY，
以B为圆心，以BC为半径画弧，交XY于P1，P2，以C为圆心，以BC为半径画弧，交XY于P3，P4，
③同理作AD的垂直平分线，
以B为圆心，以AD为半径画弧，交AB的垂直平分线于两点，以A为圆心，以AD为半径画弧，交AB的垂直平分线于两点，
即共1+4+4=9个点；
故选C．
点评 本题考查了正方形性质和等腰三角形的判定，主要考查学生的理解能力和动手操作能力，熟练掌握等腰三角形的判定定理是解题的关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
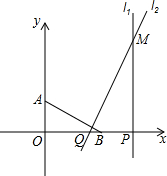如图，点A（0，1）、B（2，0），点P从（4，0）出发，以每秒2个单位长度沿x轴向坐标原点O匀速运动，同时，点Q从点B出发，以每秒1个单位长度沿x轴向坐标原点O匀速运动，过点P作x轴的垂线l，过点Q作AB的垂线l2，它们的交点为M．设运动的时间为t（0＜t＜2）秒
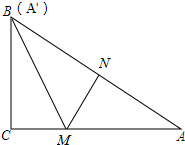如图，在Rt△ABC中，∠ACB=90°，点M在边AC上，过点M作MN⊥AB与点N，将△MNA沿着MN折叠，恰好点A的对应点A′与点B重合．