题目内容
15.已知m为整数,则关于x的方程(2+x)m+x=4的解为整数.(1)用含m的代数式表示x;
(2)求m的所有可能值.
分析 方程整理后,表示出解,根据解为正整数,确定出整数m的值即可.
解答 解:(1)由题意,得
x=$\frac{4-2m}{m+1}$,
(2)由解为整数,得m=-4,x=-4;m=-3,x=-5;m=-2,x=-8,m=0,x=4;m=1,x=1;m=2,x=0;
故m的所有可能值是-4,-3,-3,0,1,2.
点评 此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.直线l是一次函数y=kx+b的图象,点A(0,-2)、B(3,1)在直线l上,则k-b的平方根为( )
| A. | ±1 | B. | ±$\sqrt{2}$ | C. | ±$\sqrt{3}$ | D. | ±3 |
5.在解答“一元二次方程$\frac{1}{2}$x2-$\frac{1}{2}$x+a=0的根的判别式为”的过程中,某班同学的作业中出现了下面几种答案,其中正确的答案是( )
| A. | $\frac{1}{4}$-2a≥0 | B. | $\frac{1}{4}$-2a | C. | 1-8a≥0 | D. | 1-8a |
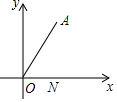 如图,点A(2,2$\sqrt{3}$),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为$\frac{3}{2}$.
如图,点A(2,2$\sqrt{3}$),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为$\frac{3}{2}$.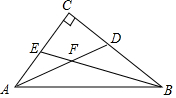 已知:如图所示,Rt△ABC中,∠C=90°,∠A、∠B的平分线AD、BE交于F,求∠AFB的度数.
已知:如图所示,Rt△ABC中,∠C=90°,∠A、∠B的平分线AD、BE交于F,求∠AFB的度数.