题目内容
1.计算:(1)(π-2011)0-$\root{3}{8}$+(sin60°)-1-|tan30°-$\sqrt{3}$|;
(2)4$\sqrt{\frac{a}{2}}$+6a$\sqrt{\frac{2}{a}}$-$\sqrt{8a}$-$\sqrt{18a}$;
(3)-22÷($\sqrt{12}$-$\sqrt{\frac{4}{5}}$)-|$\sqrt{3}-2$|;
(4)(-$\frac{1}{2}$)-1+|5-$\sqrt{27}$|-2$\sqrt{3}$+|π-sin30°|0;
(5)$\frac{tan60°-tan45°}{1+tan60°•tan45°}$+2cos30°.
分析 (1)直接利用零指数幂的性质以及负整数值幂的性质和特殊角的三角函数值以及绝对值的性质化简,进而求出答案;
(2)直接化简二次根式,进而得出答案;
(3)直接利用二次根式的性质以及绝对值的性质化简求出答案;
(4)直接利用零指数幂的性质以及负整数值幂的性质和特殊角的三角函数值以及绝对值的性质化简,进而求出答案;
(5)直接利用特殊角的三角函数值代入化简求出答案.
解答 解:(1)(π-2011)0-$\root{3}{8}$+(sin60°)-1-|tan30°-$\sqrt{3}$|
=1-2+$\frac{1}{\frac{\sqrt{3}}{2}}$-($\sqrt{3}$-$\frac{\sqrt{3}}{3}$)
=-1;
(2)4$\sqrt{\frac{a}{2}}$+6a$\sqrt{\frac{2}{a}}$-$\sqrt{8a}$-$\sqrt{18a}$
=2$\sqrt{2a}$+6$\sqrt{2a}$-2$\sqrt{2a}$-3$\sqrt{2a}$
=3$\sqrt{2a}$;
(3)-22÷($\sqrt{12}$-$\sqrt{\frac{4}{5}}$)-|$\sqrt{3}-2$|
=-4÷(2$\sqrt{3}$-$\frac{2\sqrt{5}}{5}$)-2+$\sqrt{3}$
=-$\frac{\sqrt{3}}{7}$-$\frac{\sqrt{5}}{35}$-2+$\sqrt{3}$
=$\frac{6\sqrt{3}}{7}$-$\frac{\sqrt{5}}{35}$-2;
(4)(-$\frac{1}{2}$)-1+|5-$\sqrt{27}$|-2$\sqrt{3}$+|π-sin30°|0
=-2+3$\sqrt{3}$-5-2$\sqrt{3}$+1
=-6+$\sqrt{3}$;
(5)$\frac{tan60°-tan45°}{1+tan60°•tan45°}$+2cos30°
=$\frac{\sqrt{3}-1}{1+\sqrt{3}×1}$+$\sqrt{3}$
=2-$\sqrt{3}$+$\sqrt{3}$
=2.
点评 此题主要考查了特殊角的三角函数值以及绝对值的性质、零指数幂的性质以及负整数值幂的性质等知识,正确化简各数是解题关键.

| A. | $\frac{1}{6}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{36}$ | D. | $\frac{1}{4}$ |
| A. | 30° | B. | 60° | C. | 45° | D. | 15°和75° |
| A. | 2015 | B. | 2014 | C. | 2012 | D. | 2011 |
| A. | 4.6×1010元 | B. | 0.46×1011元 | C. | 46×109元 | D. | 4.6×109元 |
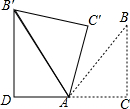 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
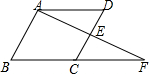 如图,在?ABCD中,过点A作AB的垂线恰好经过DC的中点E,且交BC的延长线于点F,已知AB=4cm,∠B=60°,则该平行四边形的周长是16cm.
如图,在?ABCD中,过点A作AB的垂线恰好经过DC的中点E,且交BC的延长线于点F,已知AB=4cm,∠B=60°,则该平行四边形的周长是16cm.