题目内容
12.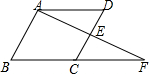 如图,在?ABCD中,过点A作AB的垂线恰好经过DC的中点E,且交BC的延长线于点F,已知AB=4cm,∠B=60°,则该平行四边形的周长是16cm.
如图,在?ABCD中,过点A作AB的垂线恰好经过DC的中点E,且交BC的延长线于点F,已知AB=4cm,∠B=60°,则该平行四边形的周长是16cm.
分析 根据平行四边形的性质得出AD=BC,AB=CD=4cm,AD∥BC,求出△ADE≌△FCE,AD=CF=BC,求出BF,即可求出AD和BC,即可得出答案.
解答 解:∵AF⊥AB,
∴∠FAB=90°,
∵∠B=60°,
∴∠F=30°,
∵AB=4cm,
∴BF=2AB=8cm,
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD=4cm,AD∥BC,
∴∠D=∠ECF,
∵E为DC的中点,
∴DE=EC,
在△ADE和△FCE中,
$\left\{\begin{array}{l}{∠D=∠ECF}\\{DE=EC}\\{∠AED=∠FEC}\end{array}\right.$,
∴△ADE≌△FCE(ASA),
∴AD=CF=BC,
∴BC=CF=4cm,
∴平行四边形的周长为AB+BC+CD+AD=4cm+4cm+4cm+4cm=16cm.
故答案为:16.
点评 本题考查了平行四边形的性质,全等三角形的性质,含30°角的直角三角形的性质的应用,能求出AD=CF和BF的长是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列说法正确的是( )
| A. | “打开电视机,正在播世界杯足球赛”是必然事件 | |
| B. | “掷一枚硬币正面朝上的概率是$\frac{1}{2}$”表示每抛掷硬币2次就有1次正面朝上 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | 甲组数据的方差S甲2=0.09,乙组数据的方差S乙2=0.56,则甲组数据比乙组数据稳定 |
7.以下各数中,填入□中能使(-$\frac{1}{2}$)×□=-2成立的是( )
| A. | -1 | B. | 2 | C. | 4 | D. | -4 |
2.据统计,2015年目前安徽的人口达到约69285000人,用科学记数法表示为( )
| A. | 6.9285×108 | B. | 69.285×106 | C. | 0.69285×108 | D. | 6.9285×107 |