题目内容
5.请阅读求绝对值不等式|x|<3和|x|>3的解集的过程:因为|x|<3,从如图1所示的数轴上看:大于-3而小于3的数的绝对值是小于3的,所以|x|<3的解集是-3<x<3;
因为|x|>3,从如图2所示的数轴上看:小大于-3的数和大于3的数的绝对值是大于3的,所以|x|>3的解集是x<-3或x>3.
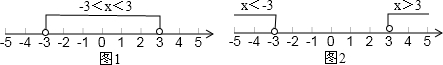
解答下面的问题:
(1)不等式|x|<a(a>0)的解集为-a<x<a;不等式|x|>a(a>0)的解集为x>a或x<-a.
(2)解不等式|x-2|<4;
(3)解不等式|x-5|>7.
分析 (1)由于|x|<3的解集是-3<x<3,|x|>3的解集是x<-3或x>3,根据它们即可确定|x|<a(a>0)和|x|>a(a>0)的解集;
(2)把x-2当做一个整体,首先利用(1)的结论可以求出x-2的取值范围,然后就可以求出x的取值范围;
(3)利用和(2)同样方法即可求出不等式的解集.
解答 解:(1)不等式|x|<a(a>0)的解集为-a<x<a,不等式|x|>a(a>0)的解集为x>a或x<-a,
故答案为:-a<x<a,x>a或x<-a;
(2)|x-2|<4,
∴-4<x-2<4,
则-2<x<6;
(3)∵|x-5|>7,
∴x-5<-7或x-5>7,
解得:x<-2或x>12
点评 此题是一个阅读题目,首先通过阅读把握题目中解题规律和方法,然后利用这些方法解决所给出的题目,所以解题关键是正确理解阅读材料的解题方法,才能比较好的解决问题.此题是一个绝对值的问题,有点难以理解,要反复阅读,充分理解题意.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | (2$\sqrt{2}$)2=4 | B. | $\sqrt{\frac{5}{2}}$=$\frac{\sqrt{5}}{2}$ | C. | $\sqrt{{x}^{2}}$=x | D. | $\sqrt{-{x}^{3}}$=-x$\sqrt{-x}$ |
10.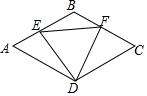 如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )
如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )
 如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )
如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )| A. | ①② | B. | ②③④ | C. | ①②③④ | D. | ①②④ |
14.在函数y=$\frac{\sqrt{x-3}}{2}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x≠3 | D. | x≤3 |
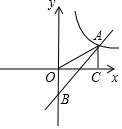 如图,点A(5,a)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限的交点,点B(0,-3)是该一次函数与y轴的交点,连结OA,过点A作AC⊥x轴,垂足为C,若Rt△AOC的面积为5.
如图,点A(5,a)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限的交点,点B(0,-3)是该一次函数与y轴的交点,连结OA,过点A作AC⊥x轴,垂足为C,若Rt△AOC的面积为5.