题目内容
12．
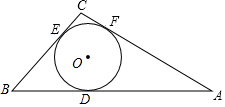如图，若△ABC的三边长分别为AB=9，BC=5，CA=6，△ABC的内切圆⊙O切AB、BC、AC于点D、E、F，则AF的长为4.5．
分析 设AF=x，依据切线长定理可得到AF=AD，CF=CE，BD=BE，然后用含x的式子表示出EC和CF的长，然后列出关于x的方程求解即可．
解答 解：设AF=x．
由切线长定理可知：AF=AD，CF=CE，BD=BE．
∵AB=9，BC=5，CA=6，
∴CF=6-x，CE=BC-BE=BC-BD=6-（9-x）=x-3．
∴6-x=x-3．
∴x=4.5．
故答案为：4.5．
点评 本题主要考查的是三角形的内切圆的性质，依据切线长定理列出关于x的方程是解题的关键．
练习册系列答案
相关题目
3．（-2）2的平方根是（ ）
| A． | ±2 | B． | -2 | C． | 2 | D． | $\sqrt{2}$ |
20．下列各式中，是一元一次方程的是（ ）
| A． | x-y=2 | B． | $\frac{x-1}{2}$=$\frac{x-2}{3}$ | C． | 2x-3 | D． | x2+x=2 |
17．一个多边形的内角和是1260°，这个多边形的边数是（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
7．
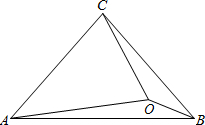△ABC中，∠CAB=∠CBA=50°，O为△ABC内一点，∠OAB=10°，∠OBC=20°，则∠OCA的度数为（ ）
△ABC中，∠CAB=∠CBA=50°，O为△ABC内一点，∠OAB=10°，∠OBC=20°，则∠OCA的度数为（ ）| A． | 55° | B． | 60° | C． | 70° | D． | 80° |
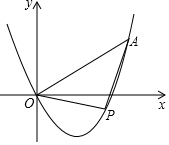如图，二次函数y=ax2-（4a-0.5）x（a＞0）的图象经过点A（4，m），若点P是这个二次函数图象上的一个动点，当△POA为等腰直角三角形时，a的值是$\frac{5}{6}$或$\frac{5}{4}$或$\frac{5}{12}$．