题目内容
13.探究并回答(1)数轴上表示3和5的两点距离是2,表示-3和5两点的距离是8.
(2)在数轴上表示a和-2的两点A和B的距离是|a+2|;(用含a的代数式表示)如果AB=3,那么a=1或-5.
(3)猜想对于有理数a,|a+1|+|a-2|能够取得的最小值是3.
分析 根据数轴的意义可知两点间的距离可以用坐标差的绝对值表示.
解答 解:(1)由题意可知:数轴上表示3和5的两点距离是5-3=2,
表示-3和5两点的距离是5-(-3)=8,
(2)在数轴上表示a和-2的两点A和B的距离是|a+2|,
当AB=3时,
∴|a+2|=3,
∴a+2=±3,
∴a=1或-5;
(3)由绝对值的定义可知:,|a+1|+|a-2|表示数a到-1和2的距离之和,
当-1≤a≤2时,
|a+1|+|a-2|可取得最小值,此时最小值为3,
故答案为:(1)2;8,
(2)|a+2|;1或-5,
(3)3
点评 本题考查数轴的定义,涉及数形结合的思想,属于中等题型.

练习册系列答案
相关题目
3.一个各面分别标有数字1,2,3,4,5,6的骰子,连续投掷二次,分别出现数字m,n,得到一个点P(m,n),则点P既在直线y=-x+5上,又在双曲线y=$\frac{6}{x}$上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{36}$ |
4.某商店为吸引顾客设计了促销活动:在一不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客一次性消费满400元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回),某顾客刚好消费400元,则该顾客获得的金额不低于30元的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |

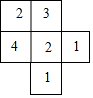 如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).
如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).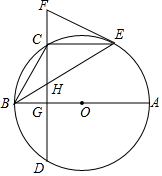 AB是⊙O的直径,点E是⊙O上一个点,C是弧BE的中点,弦CD⊥AB,G为垂足,且交BE于点H,经过点E作⊙O的切线交DC的延长线于点F.
AB是⊙O的直径,点E是⊙O上一个点,C是弧BE的中点,弦CD⊥AB,G为垂足,且交BE于点H,经过点E作⊙O的切线交DC的延长线于点F.