题目内容
3.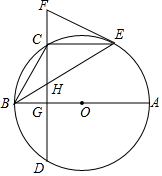 AB是⊙O的直径,点E是⊙O上一个点,C是弧BE的中点,弦CD⊥AB,G为垂足,且交BE于点H,经过点E作⊙O的切线交DC的延长线于点F.
AB是⊙O的直径,点E是⊙O上一个点,C是弧BE的中点,弦CD⊥AB,G为垂足,且交BE于点H,经过点E作⊙O的切线交DC的延长线于点F.(1)按边分类,△BCH和△EFH是什么三角形?
(2)如果CE∥AB,求∠EFD.
分析 (1)△BCH和△EFH是等腰三角形,只要证明∠HBC=∠HCB,∠FHE=∠FEH即可解决问题.
(2)如图2中,连接AC、OC、OE.首先证明$\widehat{BC}$=$\widehat{EC}$=$\widehat{AE}$,推出∠BOC=∠COE=∠AOE=60°,推出△EFH是等边三角形即可.
解答 解:(1)按边分类,△BCH和△EFH是等腰三角形.
理由:∵弦CD⊥AB,
∴$\widehat{BC}$=$\widehat{BD}$,
∵C是弧BE的中点,
∴$\widehat{CE}$=$\widehat{CB}$=$\widehat{BD}$,
∴∠BCH=∠EBH,
∴CH=BH,
即△BCH是等腰三角形;
如图1中,连接OE,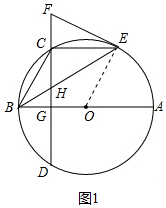
∵EF是⊙O的切线,
∴OE⊥EF,
∴∠OEB+∠FEH=90°,
∵∠EHF=∠BHG,∠BHG+∠OBE=90°,
∴∠EHF+∠OBE=90°,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠EHF=∠FEH,
∴FH=FE,
即△EFH是等腰三角形;
(2)如图2中,连接AC、OC、OE.
∵EC∥AB,
∴∠ECA=∠BAC,
∴$\widehat{AE}$=$\widehat{BC}$,
∵$\widehat{BC}$=$\widehat{EC}$,
∴$\widehat{BC}$=$\widehat{EC}$=$\widehat{AE}$,
∴∠BOC=∠COE=∠AOE=60°,
∴∠ABE=$\frac{1}{2}$∠AOE=30°,
∵CD⊥AB,
∴∠BGH=90°,∠BHG=∠FHE=60°,
∵FH=FE,
∴△FHE是等边三角形,
∴∠EFD=60°.
点评 本题考查切线的性质、垂径定理、圆周角定理、等边三角形的判定等知识,解题的关键的灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.

 智慧小复习系列答案
智慧小复习系列答案| A. | $\frac{1}{210}$ | B. | $\frac{1}{231}$ | C. | $\frac{1}{190}$ | D. | $\frac{1}{171}$ |
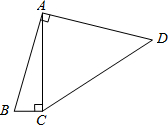 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
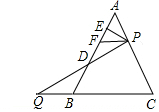 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.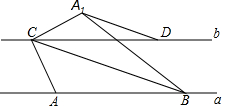 如图,已知直线a∥b,a、b之间的距离为4cm.A、B是直线a上的两个定点,C、D是直线b上的两个动点(点C在点D的左侧),且AB=CD=10cm,连接AC、BD、BC,将△ABC沿BC翻折得△A1BC.
如图,已知直线a∥b,a、b之间的距离为4cm.A、B是直线a上的两个定点,C、D是直线b上的两个动点(点C在点D的左侧),且AB=CD=10cm,连接AC、BD、BC,将△ABC沿BC翻折得△A1BC.