题目内容
4.某商店为吸引顾客设计了促销活动:在一不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客一次性消费满400元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回),某顾客刚好消费400元,则该顾客获得的金额不低于30元的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 列表法或画树状图法可以不重复不遗漏地列出所有可能的结果,适合于两步完成的事件.
解答 解:列表:
| 第二次 第一次 | 0 | 10 | 20 | 30 |
| 0 | -- | 10 | 20 | 30 |
| 10 | 10 | -- | 30 | 40 |
| 20 | 20 | 30 | -- | 50 |
| 30 | 30 | 40 | 50 | -- |
因此P(不低于30元)=$\frac{8}{12}$=$\frac{2}{3}$.
故选:C.
点评 本题主要考查用列表法或树状图求概率.解决本题的关键是弄清题意,满400元可以摸两次,但摸出一个后不放回,概率在变化.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.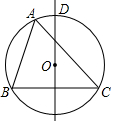 如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
 如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )| A. | 23° | B. | 28° | C. | 30° | D. | 37° |
12.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-y-1=0 | C. | $\frac{1}{x}$+x=1 | D. | x2=2 |
19.到三角形的三边距离相等的点是( )
| A. | 三角形三条高的交点 | B. | 三角形三条内角平分线的交点 | ||
| C. | 三角形三条中线的交点 | D. | 无法确定 |
9.从多边形的一个顶点出发,连接其它各个顶点得到2016个三角形,则这个多边形的边数为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
16.点A(-3,2)关于x轴对称的点是B,点B关于y轴对称的点是C,则点C的坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (-3,-2) | D. | (3,-2) |

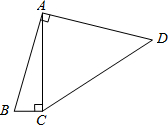 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?