题目内容
3.一个各面分别标有数字1,2,3,4,5,6的骰子,连续投掷二次,分别出现数字m,n,得到一个点P(m,n),则点P既在直线y=-x+5上,又在双曲线y=$\frac{6}{x}$上的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{36}$ |
分析 先列表得出各种可能的结果,再找出符合条件的点,根据概率公式求解即可.
解答 解:列表: ,
,
由表可知,共有36种可能的结果,点P既在直线y=-x+5又在双曲线y=$\frac{6}{x}$上的点有(2,3),(3,2),所以概率=$\frac{2}{36}$=$\frac{1}{18}$.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
13.已知ab>0,bc<0,则直线y=-$\frac{a}{b}$x+$\frac{a}{c}$经过的象限为( )
| A. | 一、二、三 | B. | 一、二、四 | C. | 二、三、四 | D. | 一、二、四 |
11.在△ACB中,AB=10,sinA=$\frac{3}{5}$,则BC的长为( )
| A. | 6 | B. | 7.5 | C. | 8 | D. | 不能确定 |
15.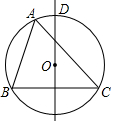 如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
 如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )
如图,⊙O是△ABC的外接圆,BC的中垂线与$\widehat{AC}$相交于D点,若∠B=74°,∠C=46°,则$\widehat{AD}$的度数为( )| A. | 23° | B. | 28° | C. | 30° | D. | 37° |
12.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-y-1=0 | C. | $\frac{1}{x}$+x=1 | D. | x2=2 |

 在如图所示的运算程序中,如果输出的数y=6,则输入的数x=2或9.
在如图所示的运算程序中,如果输出的数y=6,则输入的数x=2或9.