题目内容
1.已知关于x的方程x2+ax+a-1=0.(1)若该方程的一个根为2,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有实数根.
分析 (1)将x=2代入原方程中得出关于a的一元一次方程,解方程求出a值,再将a值代入原方程,解方程即可得出结论;
(2)由方程的各项系数结合根的判别式即可得出△=(a-2)2≥0,此题得证.
解答 (1)解:将x=2代入方程x2+ax+a-1=0中,得:4+2a+a-1=0,
解得:a=-1,
∴原方程为x2-x-2=(x+1)(x-2)=0,
解得:x1=-1,x2=2.
答:a的值为-1,方程的另一个根为-1.
(2)证明:在方程x2+ax+a-1=0中,△=a2-4(a-1)=a2-4a+4=(a-2)2≥0,
∴不论a取何实数,该方程都有实数根.
点评 本题考查了根的判别式以及一元二次方程的解,将x的值代入原方程求出a值是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
11.在△ACB中,AB=10,sinA=$\frac{3}{5}$,则BC的长为( )
| A. | 6 | B. | 7.5 | C. | 8 | D. | 不能确定 |
12.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-y-1=0 | C. | $\frac{1}{x}$+x=1 | D. | x2=2 |
9.从多边形的一个顶点出发,连接其它各个顶点得到2016个三角形,则这个多边形的边数为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
16.点A(-3,2)关于x轴对称的点是B,点B关于y轴对称的点是C,则点C的坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (-3,-2) | D. | (3,-2) |
10.(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)可以表示为( )
| A. | (-$\frac{2}{3}$)×4 | B. | -$\frac{{2}^{4}}{3}$ | C. | -($\frac{2}{3}$)4 | D. | (-$\frac{2}{3}$)4 |
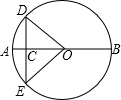 如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.
如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.