题目内容
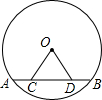已知：CD是⊙O的弦AB上的两点，且AC=BD，连接OC、OD，求证：OC=OD．考点：垂径定理,等腰三角形的判定与性质
专题：证明题
分析：连接OA、OB，过O作OE⊥AB于E，根据等腰三角形的性质求出AE=BE，求出CE=ED，根据线段垂直平分线性质求出即可．
解答：
证明：连接OA、OB，过O作OE⊥AB于E，
∵OA=OB，
∴AE=BE，
∵AC=BD，
∴CE=DE，
∵OE⊥CD，
∴OC=OD．
证明：连接OA、OB，过O作OE⊥AB于E，∵OA=OB，
∴AE=BE，
∵AC=BD，
∴CE=DE，
∵OE⊥CD，
∴OC=OD．
点评：本题考查了等腰三角形的性质，线段垂直平分线性质的应用，能正确作出辅助线，并能正确运用法则进行推理是解此题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
这是一根起点为0的数轴，现有同学将它弯折，如图所示，例如：第一行0，第二行6，第三行21…则虚线上的第10行的数是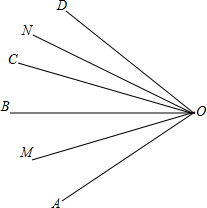
如图，OB、OC是∠AOD内的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=70°，∠BOC=30°，求∠AOD的度数．
如图，△ABO与△DOC是否相似？为什么？