题目内容
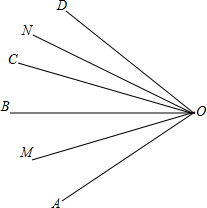 如图,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=70°,∠BOC=30°,求∠AOD的度数.
如图,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=70°,∠BOC=30°,求∠AOD的度数.考点:角平分线的定义
专题:
分析:首先根据角平分线的性质可得∠AOM=∠BOM=
∠AOB,∠DON=∠CON=
∠COD,再计算出∠NOC+∠BOM=40°,进而得到∠DOC+∠AOB=80°,从而可得∠AOD的度数.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OM平分∠AOB,ON平分∠COD,
∴∠AOM=∠BOM=
∠AOB,∠DON=∠CON=
∠COD,
∵∠MON=70°,∠BOC=30°,
∴∠NOC+∠BOM=70°-30°=40°,
∴∠DOC+∠AOB=40°×2=80°,
∴∠AOD=80°+30°=110°.
∴∠AOM=∠BOM=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠MON=70°,∠BOC=30°,
∴∠NOC+∠BOM=70°-30°=40°,
∴∠DOC+∠AOB=40°×2=80°,
∴∠AOD=80°+30°=110°.
点评:此题主要考查了角平分线的定义,关键是掌握角平分线把角分成相等的两部分.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
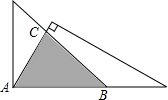 一副三角板按如图所示位置摆放,测得BC=10cm,则两个三角板重叠(阴影)部分的面积为( )
一副三角板按如图所示位置摆放,测得BC=10cm,则两个三角板重叠(阴影)部分的面积为( )| A、75m2 | ||||
B、(25+25
| ||||
C、(25+
| ||||
D、(25+
|
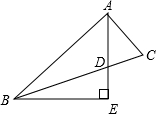 如图,AD是△ABC的角平分线,AD=AC,BE⊥AD于E
如图,AD是△ABC的角平分线,AD=AC,BE⊥AD于E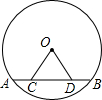 已知:CD是⊙O的弦AB上的两点,且AC=BD,连接OC、OD,求证:OC=OD.
已知:CD是⊙O的弦AB上的两点,且AC=BD,连接OC、OD,求证:OC=OD.