题目内容
20. 如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
分析 根据三角形的内角和得出∠ACB的度数,再根据角平分线的性质求出∠DCA的度数,再根据三角形内角与外角的关系求出∠BDC的度数.
解答 解:∵∠A+∠B+∠ACB=180°(三角形内角和定理),
∴∠ACB=180°-∠A-∠B=180°-80°-40°=60°,
∵CD是∠ACB的平分线,
∴$∠ACD=\frac{1}{2}$∠ACB=30°(角平分线的性质),
∴∠BDC=∠ACD+∠A=30°+80°=110°(三角形外角的性质).
故选D.
点评 本题主要考查了三角形的内角和定理,角平分线的定义及三角形外角的知识,三角形的一个外角等于与它不相邻的两个内角的和,难度适中.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
11.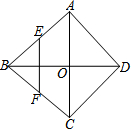 如图,菱形ABCD的对角线AC、BD相交于O点,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC、BD相交于O点,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
 如图,菱形ABCD的对角线AC、BD相交于O点,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线AC、BD相交于O点,E、F分别是AB、BC边上的中点,连接EF.若EF=$\sqrt{3}$,BD=4,则菱形ABCD的周长为( )| A. | 5 | B. | $4\sqrt{6}$ | C. | $4\sqrt{7}$ | D. | 20 |
5.若关于x的方程(1-k)x2-2x-1=0有实根,则k的取值范围是( )
| A. | k≥2 | B. | k≤2且k≠1 | C. | k≤2 | D. | k≥2且k≠1 |
12.若3a2-2b+2的值是-1,则5+4b-6a2的值是( )
| A. | 1 | B. | 4 | C. | 7 | D. | 11 |
9.计算:2x2•(-3x3)的结果是( )
| A. | -6x5 | B. | 6x5 | C. | 5x5 | D. | -5x5 |
10. 如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )
如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )
 如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )
如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )| A. | 1:40 | B. | 1:80 | C. | 1:4000 | D. | 1:8000 |
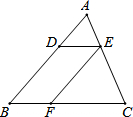 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8. 如图,∠A+∠B+∠C+∠D+∠1的度数为180°.
如图,∠A+∠B+∠C+∠D+∠1的度数为180°.