题目内容
 已知:A(2,4)、B(2,0),通过原点的直线把△AOB的面积分为1:2的两部分,求这条直线的解析式.
已知:A(2,4)、B(2,0),通过原点的直线把△AOB的面积分为1:2的两部分,求这条直线的解析式.考点:待定系数法求一次函数解析式
专题:计算题
分析:分两种情况考虑:三角形AOC面积与三角形BOC面积之比为2:1;三角形AOC面积与三角形BOC面积之比为1:2;分别确定出C坐标,利用待定系数法求出直线解析式即可.
解答: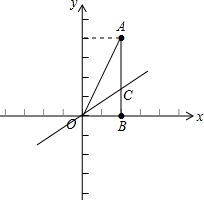 解:分两种情况考虑:当S△AOC:S△BOC=2:1时,由高相同得到AC=2BC,
解:分两种情况考虑:当S△AOC:S△BOC=2:1时,由高相同得到AC=2BC,
∵A(2,4),B(2,0),
∴AB=4,即BC=
,
∴C(2,
),
设直线OC解析式为y=kx,把C坐标代入得:
=2k,即k=
,
此时直线解析式为y=
x;
当S△AOC:S△BOC=1:2时,由高相同得到BC=2AC,
同理得到BC=
,此时C(2,
),
此时直线解析式为y=
x.
 解:分两种情况考虑:当S△AOC:S△BOC=2:1时,由高相同得到AC=2BC,
解:分两种情况考虑:当S△AOC:S△BOC=2:1时,由高相同得到AC=2BC,∵A(2,4),B(2,0),
∴AB=4,即BC=
| 4 |
| 3 |
∴C(2,
| 4 |
| 3 |
设直线OC解析式为y=kx,把C坐标代入得:
| 4 |
| 3 |
| 2 |
| 3 |
此时直线解析式为y=
| 2 |
| 3 |
当S△AOC:S△BOC=1:2时,由高相同得到BC=2AC,
同理得到BC=
| 8 |
| 3 |
| 8 |
| 3 |
此时直线解析式为y=
| 4 |
| 3 |
点评:此题考查了待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
下列说法中,正确的有( )
①在同圆或等圆中,相等的弦所对的弧相等;
②在同圆或等圆中,相等的弦所对的弧心距相等
③在同圆或等圆中,相等的弦所对的圆周角相等
④在同圆或等圆中,相等的弦所对的圆心角相等.
①在同圆或等圆中,相等的弦所对的弧相等;
②在同圆或等圆中,相等的弦所对的弧心距相等
③在同圆或等圆中,相等的弦所对的圆周角相等
④在同圆或等圆中,相等的弦所对的圆心角相等.
| A、1个 | B、2个 | C、3个 | D、4个 |
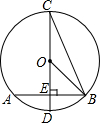 如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、CD,已知⊙O的半径为2,AB=2
如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、CD,已知⊙O的半径为2,AB=2| 3 |
| A、30° | B、45° |
| C、60° | D、15° |
 某校有一块长方形操场如图所示,长为x m,宽为y m.为了美化校园环境,学校决定在操场四周修a m宽的绿化带,以剩下操场的面积决定绿化带的宽度,求剩下操场的面积.
某校有一块长方形操场如图所示,长为x m,宽为y m.为了美化校园环境,学校决定在操场四周修a m宽的绿化带,以剩下操场的面积决定绿化带的宽度,求剩下操场的面积.