题目内容
2．某果园2014年水果产量为100吨，2016年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x，则根据题意可列方程为（ ）| A． | 144（1-x）2=100 | B． | 100（1-x）2=144 | C． | 144（1+x）2=100 | D． | 100（1+x）2=144 |
分析 2016年的产量=2012年的4量×（1+年平均增长率）2，把相关数值代入即可；
解答 解：设该果园水果产量的年平均增长率为x，则201年5的产量为100（1+x）吨，2016年的产量为100（1+x）（1+x）=100（1+x）2吨，
根据题意，得100（1+x）2=144，
故选：C．
点评 本题考查了由实际问题抽象出一元二次方程；得到2016年产量的等量关系是解决本题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，-1）、B（-1，1）、C（0，-2）．
13．已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（ ）
| A． | 不能确定 | B． | 相离 | C． | 相切 | D． | 相交 |
10．对于函数y=-x2+2x-2，使得y随x的增大而增大的x的取值范围是（ ）
| A． | x＞1 | B． | x≥0 | C． | x≤0 | D． | x＜1 |
7．
如图所示，△ABC中，AB+BC=10，A、C关于直线DE对称，则△BCD的周长是（ ）
如图所示，△ABC中，AB+BC=10，A、C关于直线DE对称，则△BCD的周长是（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 无法确定 |
14．
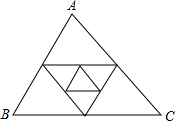如图，已知△ABC的周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形三边的中点构成第三个三角形，依此类推，则第2016个三角形的周长为（ ）
如图，已知△ABC的周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形三边的中点构成第三个三角形，依此类推，则第2016个三角形的周长为（ ）| A． | $\frac{1}{2015}$ | B． | $\frac{1}{2016}$ | C． | $\frac{1}{{2}^{2015}}$ | D． | $\frac{1}{{2}^{2016}}$ |
11．在△ABC中，∠A=30°，∠B=50°，则∠C为（ ）
| A． | 30° | B． | 50° | C． | 80° | D． | 100° |