题目内容
10.对于函数y=-x2+2x-2,使得y随x的增大而增大的x的取值范围是( )| A. | x>1 | B. | x≥0 | C. | x≤0 | D. | x<1 |
分析 先运用配方法将抛物线写成顶点式y=-(x+1)2-1,由于a=-1<0,抛物线开口向下,对称轴为直线x=1,根据抛物线的性质可知当x<1时,y随x的增大而增大,即可求出.
解答 解:∵y=-x2+2x-2=-(x-1)2-1,
a=-1<0,抛物线开口向下,对称轴为直线x=-1,
∴当x<1时,y随x的增大而增大,
故选D.
点评 本题考查了二次函数y=ax2+bx+c(a≠0)的性质,确定抛物线的对称轴是解答本题的关键,a>0,抛物线开口向上,在对称轴左侧y随x的增大而减小;a<0,抛物线开口向下,在对称轴左侧y随x的增大而增大.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.如果两个有理数的和为负数,积为正数,那么这两个有理数( )
| A. | 都是正数 | B. | 都是负数 | C. | 是一正一负 | D. | 无法确定 |
18.计算4×(-2)的结果是( )
| A. | 8 | B. | -8 | C. | 6 | D. | -2 |
5.在代数式$\frac{1}{2}$x-y,5a,x2-y+$\frac{2}{3}$,$\frac{1}{π}$,xyz,-$\frac{5}{y}$,$\frac{x+y+z}{3}$中,有( )
| A. | 5个整式 | |
| B. | 4个单项式,3个多项式 | |
| C. | 6个整式,4个单项式 | |
| D. | 6个整式,单项式与多项式的个数相同 |
2.某果园2014年水果产量为100吨,2016年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
| A. | 144(1-x)2=100 | B. | 100(1-x)2=144 | C. | 144(1+x)2=100 | D. | 100(1+x)2=144 |
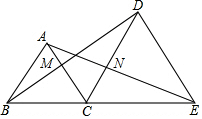 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.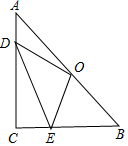 在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.
在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.