题目内容
17.我们知道:圆周角的度数等于它所对弧上的圆心角度数的一半.(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③证明上述结论;

(2)证明上述结论,运用的数学思想方法有:分类讨论.
(3)我们把“顶点在圆外的角”称之为“圆外角”,把“顶点在圆内的角”称之为“圆内角”,“圆外角”或“圆内角”是否依然等于“它所对弧上的圆心角度数的一半”?请你分别结合图④、⑤对你的结论加以说明.
分析 (1)利用等腰三角形的两底角相等以及三角形的外角的性质即可证得;
(2)分成三种不同情况,则利用了分类讨论思想;
(3)作出∠AOC对应的圆周角,利用(1)的结论好三角形的外角的性质即可解答.
解答 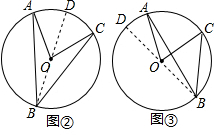 解:(1)在图①中,∵OA=OB,
解:(1)在图①中,∵OA=OB,
∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠B=$\frac{1}{2}$∠AOC;
在图②中,作直径BD,同①可得∠ABD=$\frac{1}{2}$∠AOD,∠CBD=$\frac{1}{2}$∠COD,
则∠ABC=$\frac{1}{2}$∠AOC;
在图③中,作直径BD.
同理∠CBD=$\frac{1}{2}$∠COD,∠ABD=$\frac{1}{2}$∠AOD,
∴∠ABC=∠CBD-∠ABD=$\frac{1}{2}$∠COD-$\frac{1}{2}$∠AOD=$\frac{1}{2}$(∠COD-∠AOD)=$\frac{1}{2}$∠AOC;
(2)运用了分类讨论思想.
故答案是:分类讨论;
(3)圆外角”或“圆内角”不等于“它所对弧上的圆心角度数的一半”.
如图④.
连接CD.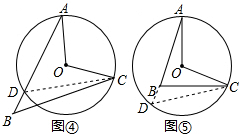
根据(1)可得∠ADC=$\frac{1}{2}$∠AOC,
又∵∠ADC>∠B,
∴∠B<$\frac{1}{2}$∠AOC;
在图⑤中,延长AB交圆于点D,连接CD.
∵∠D=$\frac{1}{2}$∠AOC,
又∵∠D<∠ABC,
∴∠ABC>$\frac{1}{2}$∠AOC.
点评 本题考查了圆周角定理的证明,以及等腰三角形的性质,正确进行分类讨论是关键.

练习册系列答案
相关题目
8.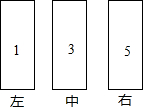 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )
如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第200拍时,你听到的是( )| A. | 同样的音“1” | B. | 同样的音“3” | C. | 同样的音“5” | D. | 不同的两个音 |
9.已知二次函数y=kx2-2x-1的图象和x轴有交点,则k的取值范围是( )
| A. | k>-1 | B. | k<1 | C. | k≥-l且k≠0 | D. | k<1且k≠0 |
 如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:
如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明: 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.