题目内容
9.已知二次函数y=kx2-2x-1的图象和x轴有交点,则k的取值范围是( )| A. | k>-1 | B. | k<1 | C. | k≥-l且k≠0 | D. | k<1且k≠0 |
分析 由于二次函数与x轴有交点,故二次函数对应的一元二次方程kx2-2x-1=0中,△≥0,解不等式即可求出k的取值范围,由二次函数定义可知k≠0.
解答 解:∵二次函数y=kx2-2x-1的图象和x轴有交点,
∴△=b2-4ac=4-4×k×(-1)≥0,且k≠0,
∴k≥-1,且k≠0.
故选C.
点评 本题考查了了抛物线与x轴的交点,利用根的判别式得出不等式是解题关键.

练习册系列答案
相关题目
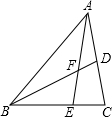 如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).
如图,在△ABC中,D、E分别为AC、BC边上一点,AE与BD交于点F.已知AD=CD,BE=2CE,且△ABC的面积为60平方厘米,则△ADF的面积为6平方厘米;如果把“BE=2CE”改为“BE=nCE”其余条件不变,则△ADF的面积为$\frac{30}{2n+1}$平方厘米(用含n的代数式表示).
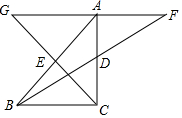 BD、CE是△ABC的中线,分别在BD、CE的延长线上截取DF=DB、EG=EC,连接AF、AG.求证:AF=AG.
BD、CE是△ABC的中线,分别在BD、CE的延长线上截取DF=DB、EG=EC,连接AF、AG.求证:AF=AG. 如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,其中点B坐标为(4,3).
如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,其中点B坐标为(4,3).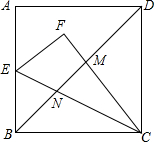 在正方形ABCD中,AD=4.点E是线段AB的中点,连接CE,将△BCE沿CE翻折,使点B落在点F处,对角线BD与CF,CE分别相交于点M,N,则MN的长是$\frac{20}{21}\sqrt{2}$..
在正方形ABCD中,AD=4.点E是线段AB的中点,连接CE,将△BCE沿CE翻折,使点B落在点F处,对角线BD与CF,CE分别相交于点M,N,则MN的长是$\frac{20}{21}\sqrt{2}$..