Question

3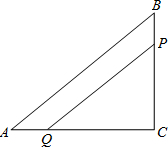．如图，在Rt△ABC中，∠C=90°，AC=7，BC=5，点P从点B开始沿BC以1单位/秒的速度向C点运动，同时点Q从点C开始沿CA以2单位/秒的速度向A点运动（当有一点到达重点时，运动随即停止）．
（1）几秒后，线段PQ的长为5？
（2）几秒后，△CPQ的面积为6？
（3）是否存在某一时刻，线段PQ的长度最小？若存在，求P、Q运动的时间；若不存在，请说明理由；
（4）是否存在某一时刻，△CPQ的面积最大？若存在，求P、Q运动时间；若不存在，请说明理由．

Answer 1

分析 设运动时间为t秒，由运动速度可知，BP=t，CQ=2t，则PC=5-t．
（1）在Rt△CPQ中，由勾股定理列方程求t的值；
（2）在Rt△CPQ中，利用面积公式列方程求t的值．
（3）得到有关PQ²的二次函数求得最值后开方即可；
（4）确定S关于t的二次函数，然后求最值即可．

解答 解：（1）设运动时间为t秒，则BP=t，CQ=2t，PC=5-t，
在Rt△CPQ中，CQ²+CP²=PQ²，即（2t）²+（5-t）²=5²，
解得t₁=0（舍去），t₂=2．
所以，2秒后，线段PQ的长为5；

（2）在Rt△CPQ中，S_△CPQ=$\frac{1}{2}$×CQ×CP，
即$\frac{1}{2}$×2t×（5-t）=6，
整理，得t²-5t+6=0，
解得t₁=2，t₂=3，
检验：当t=2或3时，CQ=2t＜7，CP=5-t＞0，符合题意．
所以，2秒或3秒后，△CPQ的面积为6．
（3）∵PQ2=4t²++（5-t）²=5（t-1）2+20≥20，
∴当t=1时，有最小值为2$\sqrt{5}$；
（4）∵S=$\frac{1}{2}$（5-t）×2t=-t²+5t，
∴当t=$\frac{5}{2}$时S最大．

点评 本题考查了一元二次方程的应用，勾股定理的应用．关键是在直角三角形中，运用运动速度表示两直角边的长，运用勾股定理和三角形面积公式解题．