题目内容
13.用符号“>”或“<”填空:(1)$\frac{6}{7}$<$\frac{7}{8}$,$\frac{6π}{7}$<$\frac{7π}{8}$;
(2)$\frac{4}{31}$<$\frac{1}{7}$,-$\frac{4}{31}$>-$\frac{1}{7}$;
(3)设a<b,则a+2<b+2,a-1<b-1,a-1<b+1;
(4)设a<b,则2a<2b,-2a>-2b,3a-1<3b-1.
分析 (1)先进行实数比较$\frac{6}{7}$与$\frac{7}{8}$的大小,然后利用不等式的性质比较$\frac{6π}{7}$与$\frac{7π}{8}$的大小;
(2)先进行实数比较$\frac{4}{31}$与$\frac{1}{7}$的大小,然后利用不等式的性质比较-$\frac{4}{31}$与-$\frac{1}{7}$的大小;
(3)根据不等式的性质求解;
(4)根据不等式的性质求解.
解答 解:(1)$\frac{6}{7}$<$\frac{7}{8}$,$\frac{6π}{7}$<$\frac{7π}{8}$;
(2)$\frac{4}{31}$<$\frac{1}{7}$,-$\frac{4}{31}$>-$\frac{1}{7}$;
(3)设a<b,则a+2<b+2,a-1<b-1,a-1<b+1;
(4)设a<b,则2a<2b,-2a>-2b,3a-1<3b-1.
故答案为<,<;<,>;<,<,<;<,>,<.
点评 本题考查了不等式的基本性质:不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,即:若a>b,那么a±m>b±m; 不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变,即:若a>b,且m>0,那么am>bm或am>bm;不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,即:若a>b,且m<0,那么am<bm或am<bm.

练习册系列答案
相关题目
3. 如图,△ABC≌△DEF,BE=2,AE=1,则BD的长是( )
如图,△ABC≌△DEF,BE=2,AE=1,则BD的长是( )
 如图,△ABC≌△DEF,BE=2,AE=1,则BD的长是( )
如图,△ABC≌△DEF,BE=2,AE=1,则BD的长是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
1.绝对值大于-2且小于5的所有的整数的和是( )
| A. | 7 | B. | -7 | C. | 0 | D. | 5 |
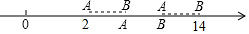 如图,在数轴上有一条可以移动的线段AB,若将线段AB向右移动,使得点A移动到点B的处,这时点B对应的数字是14,若将线段AB向左移动,使得点B移动到点A处,这时点A对应的数字是2,如果数轴的单位长度是1cm.
如图,在数轴上有一条可以移动的线段AB,若将线段AB向右移动,使得点A移动到点B的处,这时点B对应的数字是14,若将线段AB向左移动,使得点B移动到点A处,这时点A对应的数字是2,如果数轴的单位长度是1cm.