题目内容
4.已知|2014-m|+$\sqrt{m-2015}$=m,则m-20142=2015.分析 根据二次根式有意义的条件可得m-2015≥0,解不等式可得m的取值范围,然后再去绝对值可得m-2014+$\sqrt{m-2015}$=m,再整理可得答案.
解答 解:由题意得:m-2015≥0,
解得:m≥2015,
|2014-m|+$\sqrt{m-2015}$=m,
m-2014+$\sqrt{m-2015}$=m,
$\sqrt{m-2015}$=2014,
m-20142=2015,
故答案为:2015.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.为了积极开展“阳光一小时”课外活动,学校购买了一批篮球和排球,已知每个排球比篮球便宜5元,各年级分配的金额和数量如表:
(1)求篮球和排球的单价及a的值;
(2)求b、c的值.
| 年级 | 金额 | 篮球数 | 排球数 |
| 七年级 | 190元 | 3 | 4 |
| 八年级 | 220元 | 4 | a |
| 九年级 | 325元 | b | c |
(2)求b、c的值.
19.计算-2-(-3)的结果是( )
| A. | 1 | B. | -1 | C. | -5 | D. | -6 |
9.下列正确的是( )
| A. | 34<43 | B. | -34<(-4)3 | C. | -32>(-3)2 | D. | (-3×2)2<-3×22 |
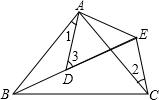 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=30°,则∠3=50°.
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=30°,则∠3=50°.