题目内容
17.当-1≤a≤1时,代数式$\sqrt{4ax+x+1}$总有意义,则x的取值范围是x$\left\{\begin{array}{l}{≤-\frac{1}{4a+1}(a<-\frac{1}{4})}\\{=全体实数(a=\frac{1}{4})}\\{>-\frac{1}{4a+1}(a>-\frac{1}{4})}\end{array}\right.$.分析 根据a的取值范围得到(4a+1)的取值范围,然后由二次根式的被开方数是非负数来求x的取值范围.
解答 解:∵-1≤a≤1,
∴-3≤4a+1≤5,
∵4ax+x+1≥0总有意义,
∴(4a+1)x≥-1总有意义,
①当4a+1<0,即a<-$\frac{1}{4}$时,x≤-$\frac{1}{4a+1}$;
②当4a+1=0,即a=-$\frac{1}{4}$时,x取全体实数;
③当4a+1>0,即a>-$\frac{1}{4}$时,x≥-$\frac{1}{4a+1}$.
综上所述,x$\left\{\begin{array}{l}{≤-\frac{1}{4a+1}(a<-\frac{1}{4})}\\{=全体实数(a=\frac{1}{4})}\\{>-\frac{1}{4a+1}(a>-\frac{1}{4})}\end{array}\right.$.
故答案是:x$\left\{\begin{array}{l}{≤-\frac{1}{4a+1}(a<-\frac{1}{4})}\\{=全体实数(a=\frac{1}{4})}\\{>-\frac{1}{4a+1}(a>-\frac{1}{4})}\end{array}\right.$.
点评 本题考查了二次根式有意义的条件.式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
相关题目
6.已知圆周率π=3.1415926…,将π精确到千分位的结果是( )
| A. | 3.1 | B. | 3.14 | C. | 3.141 | D. | 3.142 |
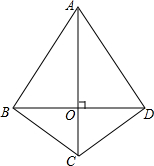 如图,AC、BD相交于点O,且AB=AD.求证:
如图,AC、BD相交于点O,且AB=AD.求证: