题目内容
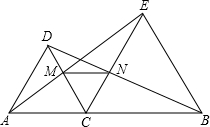 如图,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
如图,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:(1)AE=BD;
(2)CM=CN;
(3)△CMN为等边三角形;
(4)MN∥BC.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边三角形的性质得出AC=DC,EC=BC,∠ACD=∠BCE=60°,求出∠ACE=∠DCB,根据SAS推出△ACE≌△DCB即可;
(2)根据全等三角形的性质得出∠CAE=∠CDB,根据等边三角形的性质得出AC=DC,∠ACM=∠BCE=60°,求出∠DCE=60°,推出∠ACM=∠DCN,根据ASA推出△ACM≌△DCN即可;
(3)根据有一个角等于60°的等腰三角形是等边三角形推出△CMN为等边三角形,推出∠CMN=∠CNM=∠DCN=60°,求出∠CMN=∠ACM=60°,即可得出答案;
(4)根据等边三角形的性质得出∠CMN=∠ACM=60°,根据平行线的判定得出即可.
(2)根据全等三角形的性质得出∠CAE=∠CDB,根据等边三角形的性质得出AC=DC,∠ACM=∠BCE=60°,求出∠DCE=60°,推出∠ACM=∠DCN,根据ASA推出△ACM≌△DCN即可;
(3)根据有一个角等于60°的等腰三角形是等边三角形推出△CMN为等边三角形,推出∠CMN=∠CNM=∠DCN=60°,求出∠CMN=∠ACM=60°,即可得出答案;
(4)根据等边三角形的性质得出∠CMN=∠ACM=60°,根据平行线的判定得出即可.
解答:证明:(1)∵△DAC、△EBC均是等边三角形,
∴AC=DC,EC=BC,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
在△ACE和△DCB中
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)∵由(1)可知:△ACE≌△DCB,
∴∠CAE=∠CDB,
即∠CAM=∠CDN,
∵△DAC、△EBC均是等边三角形,
∴AC=DC,∠ACM=∠BCE=60°,
又点A、C、B在同一条直线上,
∴∠DCE=180°-∠ACD-∠BCE=180°-60°-60°=60°,
即∠DCN=60°,
∴∠ACM=∠DCN,
在△ACM和△DCN中
∴△ACM≌△DCN(ASA),
∴CM=CN;
(3)∵由(2)可知CM=CN,∠MCN=60°,
∴△CMN为等边三角形(有一个角等于60°的等腰三角形是等边三角形);
(4)∵△CMN为等边三角形
∴∠CMN=∠CNM=∠DCN=60°,
∴∠CMN=∠ACM=60°,
∴MN∥BC.
∴AC=DC,EC=BC,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
在△ACE和△DCB中
|
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)∵由(1)可知:△ACE≌△DCB,
∴∠CAE=∠CDB,
即∠CAM=∠CDN,
∵△DAC、△EBC均是等边三角形,
∴AC=DC,∠ACM=∠BCE=60°,
又点A、C、B在同一条直线上,
∴∠DCE=180°-∠ACD-∠BCE=180°-60°-60°=60°,
即∠DCN=60°,
∴∠ACM=∠DCN,
在△ACM和△DCN中
|
∴△ACM≌△DCN(ASA),
∴CM=CN;
(3)∵由(2)可知CM=CN,∠MCN=60°,
∴△CMN为等边三角形(有一个角等于60°的等腰三角形是等边三角形);
(4)∵△CMN为等边三角形
∴∠CMN=∠CNM=∠DCN=60°,
∴∠CMN=∠ACM=60°,
∴MN∥BC.
点评:本题考查了全等三角形的性质和判定,等边三角形的性质和判定,平行线的判定的应用,主要考查学生的运用性质进行推理的能力,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 写出如图格点△ABC各顶点的坐标,求出此三角形的周长.
写出如图格点△ABC各顶点的坐标,求出此三角形的周长.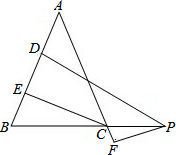 如图,在△ABC中,AB=AC,P为BC延长线上的一点,PD⊥AB,PF⊥AC,CE⊥AB,PD=7,PF=3,则CE=
如图,在△ABC中,AB=AC,P为BC延长线上的一点,PD⊥AB,PF⊥AC,CE⊥AB,PD=7,PF=3,则CE= 坡坪政府计划修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等.
坡坪政府计划修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等.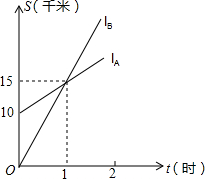 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.