题目内容
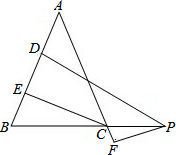 如图,在△ABC中,AB=AC,P为BC延长线上的一点,PD⊥AB,PF⊥AC,CE⊥AB,PD=7,PF=3,则CE=
如图,在△ABC中,AB=AC,P为BC延长线上的一点,PD⊥AB,PF⊥AC,CE⊥AB,PD=7,PF=3,则CE=考点:等腰三角形的性质,三角形的面积
专题:
分析:连接PA,根据三角形的面积即可得出S△PAB=S△ABC+S△PAC,进而得出PD=CE+PF,即可得出CE=4.
解答: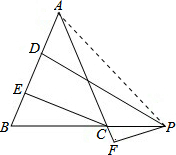 解:连接PA,
解:连接PA,
∵PD⊥AB,PF⊥AC,CE⊥AB,
∴S△PAB=
AB•PD,S△ABC=
AB•CE,S△PAC=
AC•PF,
∵S△PAB=S△ABC+S△PAC,
∴
AB•PD=
AB•CE+
AC•PF,
∵AB=AC,PD=7,PF=3
∴CE=PD-PF=7-3=4.
故答案为:4.
 解:连接PA,
解:连接PA,∵PD⊥AB,PF⊥AC,CE⊥AB,
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△PAB=S△ABC+S△PAC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,PD=7,PF=3
∴CE=PD-PF=7-3=4.
故答案为:4.
点评:本题考查了等腰三角形的性质,三角形的面积的求法,连接PA,得出S△PAB=S△ABC+S△PAC是本题的关键.

练习册系列答案
相关题目
若
+(y-2)2=0,则x-y的值为( )
| x-1 |
| A、3 | B、-3 | C、1 | D、-1 |
某邮票发行量为1250000枚,用科学记数法表示正确的是( )
| A、1.25×107枚 |
| B、1.25×106枚 |
| C、1.25×105枚 |
| D、1.25×108枚 |
 抛物线的图象如图,求这条抛物线的解析式.(结果化成一般式)
抛物线的图象如图,求这条抛物线的解析式.(结果化成一般式) 如图,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
如图,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,求证: 如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=110°,则∠A=
如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=110°,则∠A= 如图,∠DAB=∠EAC,AB=AD,AC=AE.
如图,∠DAB=∠EAC,AB=AD,AC=AE.