题目内容
写出如图格点△ABC各顶点的坐标，求出此三角形的周长．考点：勾股定理,坐标与图形性质
专题：
分析：根据各点在坐标系中的位置写出各点坐标，再根据勾股定理求出各边的长，进而可得出周长．
解答：解：由图可知，A（2，2），B（-2，-1），C（3，-2）．
AB=
=5，
AC=
=
，
BC=
=
，
故周长=5+
+
．
AB=
| 32+42 |
AC=
| 12+42 |
| 17 |
BC=
| 12+52 |
| 26 |
故周长=5+
| 17 |
| 26 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
考前必练系列答案
相关题目
若
+（y-2）2=0，则x-y的值为（ ）
| x-1 |
| A、3 | B、-3 | C、1 | D、-1 |
某邮票发行量为1250000枚，用科学记数法表示正确的是（ ）
| A、1.25×107枚 |
| B、1.25×106枚 |
| C、1.25×105枚 |
| D、1.25×108枚 |
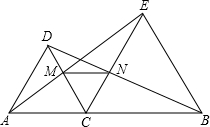如图，△DAC、△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，求证：