题目内容
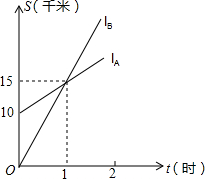 如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发与A相距
(2)B出发后
(3)分别求出A、B行走的路程S与时间t的函数关系式.
(4)出发2时,A、B之间的距离是多?
(5)通过计说明谁到达30千米处?
考点:一次函数的应用
专题:
分析:(1)利用函数图象直接得出答案;
(2)利用函数图象直接得出答案;
(3)分别利用待定系数法求一次函数解析式和正比例函数解析式即可;
(4)将t=2分别代入函数解析式求出即可;
(5)利用S=30进而求出答案.
(2)利用函数图象直接得出答案;
(3)分别利用待定系数法求一次函数解析式和正比例函数解析式即可;
(4)将t=2分别代入函数解析式求出即可;
(5)利用S=30进而求出答案.
解答:解:(1)由图象可得:B出发时与A相距10千米.
故答案为:10;
(2)由图象可得出:B出发后1小时与A相遇.
故答案为:1;
(3)设SA=kt+b,将(0,10),(1,15)代入得出:
,
解得:
故:SA=5t+10;
设SB=at,将(1,15)代入得出:
a=15,
则 SB=15t;
(4)由题意可得:SA=5×2+10=20,
SB=15×2=30,
故30-20=10(km);
(5)当30=5t+10,
解得:t=4,
当30=15t,
解得:t=2,
故2<4,B先到达30km.
故答案为:10;
(2)由图象可得出:B出发后1小时与A相遇.

故答案为:1;
(3)设SA=kt+b,将(0,10),(1,15)代入得出:
|
解得:
|
故:SA=5t+10;
设SB=at,将(1,15)代入得出:
a=15,
则 SB=15t;
(4)由题意可得:SA=5×2+10=20,
SB=15×2=30,
故30-20=10(km);
(5)当30=5t+10,
解得:t=4,
当30=15t,
解得:t=2,
故2<4,B先到达30km.
点评:此题主要考查了一次函数的应用,正确利用待定系数法求出一次函数解析式是解题关键.

练习册系列答案
相关题目
若
+(y-2)2=0,则x-y的值为( )
| x-1 |
| A、3 | B、-3 | C、1 | D、-1 |
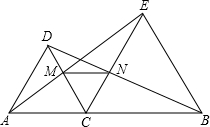 如图,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
如图,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,求证: 如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=110°,则∠A=
如图,⊙O是△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∠DOE=120°,∠EOF=110°,则∠A= 如图,在⊙O中,将△OAB绕点O顺时针方向旋转85°,得到△OCD.若∠BOA=45°,则∠BOC的度数为
如图,在⊙O中,将△OAB绕点O顺时针方向旋转85°,得到△OCD.若∠BOA=45°,则∠BOC的度数为
 如图,∠DAB=∠EAC,AB=AD,AC=AE.
如图,∠DAB=∠EAC,AB=AD,AC=AE.