题目内容
8.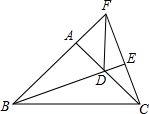 如图,△ABC中,∠BAC=90°,BD是∠ABC的平分线,BD⊥CF交CF于点E,直线CE交BA的延长线于点F且AD=AF.
如图,△ABC中,∠BAC=90°,BD是∠ABC的平分线,BD⊥CF交CF于点E,直线CE交BA的延长线于点F且AD=AF.(1)求证:△BAD≌△CAF;
(2)连接DF,若BF=15cm,求△ADF的周长.
分析 (1)先求出∠ADB=∠AFC,根据ASA即可证明△BAD≌△CAF;
(2)由△BAD≌△CAF得出AB=AC,得出∠ABC=∠ACB=45°,再证出∠AFC=∠BCE,得出AF=BC,证出BE垂直平分CF,得出DF=DC,即可得出△ADF的周长=AF+AD+DF=BF.
解答 (1)证明:∵∠BAC=90°,
∴∠CAF=90°,∠ABD+∠ADB=90°,
∵BE⊥CF,
∴∠BEF=90°,
∴∠ABD+∠AFC=90°,
∴∠ADB=∠AFC,
在△BAD和△CAF中,
$\left\{\begin{array}{l}{∠BAD=∠CAF=90°}&{\;}\\{AD=AF}&{\;}\\{∠ADB=∠AFC}&{\;}\end{array}\right.$,
∴△BAD≌△CAF(ASA);
(2)解:∵△BAD≌△CAF,
∴AB=AC,
∴∠ABC=∠ACB=45°,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABCD=22.5°,
∴∠AFC=∠BCE=90°-22.5°=67.5°,
∴AF=BC,
∴BE垂直平分CF,
∴DF=DC,
∴△ADF的周长=AF+AD+DF=AF+AD+DC=AF+AC=AF+AB=BF=15cm.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、线段垂直平分线的性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.在下列实数中,无理数是( )
| A. | $\sqrt{6}$ | B. | 3.14 | C. | 1 | D. | $\frac{1}{3}$ |
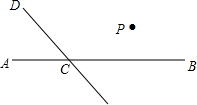 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图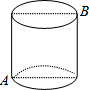 如图,己知圆柱底面周长为24cm,高为9cm,则蚂蚁在圆柱表面从A点爬到B点的最短路程是15cm.
如图,己知圆柱底面周长为24cm,高为9cm,则蚂蚁在圆柱表面从A点爬到B点的最短路程是15cm.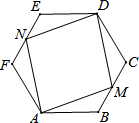 如图,正六边形ABCDEF的边长为1,M、N分别为边BC、EF的中点,则四边形AMDN的面积为$\sqrt{3}$.
如图,正六边形ABCDEF的边长为1,M、N分别为边BC、EF的中点,则四边形AMDN的面积为$\sqrt{3}$.