题目内容
已知a、b是方程x2-x-2=0的两个不相等实数根,则a•b的值是 .
考点:根与系数的关系
专题:
分析:由a,b是方程x2-x-2=0的两个不相等的实数根,利用根与系数的关系即可求出两根之积.
解答:解:∵a、b是方程x2-x-2=0的两个不相等实数根,
∴a•b=-2.
故答案为:-2.
∴a•b=-2.
故答案为:-2.
点评:此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当方程有解,即b2-4ac≥0时,设方程的解分别为x1,x2,则有x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
在平面直角坐标系中,点(-5,2)所在的象限为( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
方程(x+1)(x-2)=x-2的解为( )
| A、x=0 |
| B、x=-1 |
| C、x1=2,x2=-1 |
| D、x1=0,x2=2 |

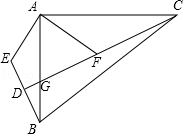 如图,在△ABC中,∠BAC=90°,∠EAF=90°,AB•AF=AC•AE.连接CF并延长CF交AB于点G,交BE于点D.
如图,在△ABC中,∠BAC=90°,∠EAF=90°,AB•AF=AC•AE.连接CF并延长CF交AB于点G,交BE于点D.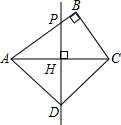 如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一点,且AD是AP与AB的比例中项.求证:
如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一点,且AD是AP与AB的比例中项.求证: