题目内容
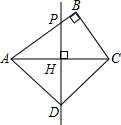 如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一点,且AD是AP与AB的比例中项.求证:
如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一点,且AD是AP与AB的比例中项.求证:(1)AP•AB=AH•AC;
(2)△ACD是等腰直角三角形.
考点:相似三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)根据线段垂直平分线的性质得∠AHD=90°,CD=AD,根据两组角对应相等的两个三角形相似易得△APH∽△ACB,则
=
,然后利用比例的性质即可得到结论;
(2)由AD是AP与AB的比例中项得AD2=AP•AB,加上(1)的结论可得AH•AC=AD2,写成比例式为
=
,加上∠DAH=∠CAD,于是根据相似三角形的判定得到可得△ADH∽△ACD,所以∠ADC=∠AHD=90°,由于CD=AD,于是可判断△ACD是等腰直角三角形.
| AP |
| AC |
| AH |
| AB |
(2)由AD是AP与AB的比例中项得AD2=AP•AB,加上(1)的结论可得AH•AC=AD2,写成比例式为
| AD |
| AC |
| AH |
| AD |
解答:证明:(1)∵PH是AC的垂直平分线,
∴∠AHD=90°,CD=AD,
∴∠PHA=∠B=90°,
∵∠PAH=∠BAC,
而∠PAH=∠CAB,
∴△APH∽△ACB,
∴
=
,
∴AH•AC=AP•AB;
(2)∵AD是AP与AB的比例中项,
∴AD2=AP•AB,
∴AH•AC=AD2,
∴
=
,
∵∠DAH=∠CAD,
∴△ADH∽△ACD,
∴∠ADC=∠AHD=90°,
∵CD=AD,
∴△ACD是等腰直角三角形.
∴∠AHD=90°,CD=AD,
∴∠PHA=∠B=90°,
∵∠PAH=∠BAC,
而∠PAH=∠CAB,
∴△APH∽△ACB,
∴
| AP |
| AC |
| AH |
| AB |
∴AH•AC=AP•AB;
(2)∵AD是AP与AB的比例中项,
∴AD2=AP•AB,
∴AH•AC=AD2,
∴
| AD |
| AC |
| AH |
| AD |
∵∠DAH=∠CAD,
∴△ADH∽△ACD,
∴∠ADC=∠AHD=90°,
∵CD=AD,
∴△ACD是等腰直角三角形.
点评:本题考查了相似三角形的判定与性质:灵活运用三角形相似的判定定理;理解比例中项的定义和线段垂直平分线的性质;掌握等腰直角三角形的判定方法.

练习册系列答案
相关题目
河南省卫生计生委2014年新农合实施情况最新发布:数字显示,去年河南省累计补偿住院医疗费用250.56亿元,广大人民群众享受到新农合政策带来的好处.下面对“250.56亿”科学记数正确的是( )
| A、2.5056×1010 |
| B、2.5056×109 |
| C、2.5056×108 |
| D、2.5056×107 |
2.6万是精确到( )
| A、百分位 | B、千位 |
| C、十分位 | D、百位 |
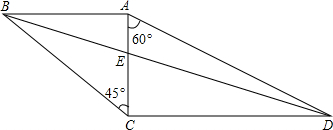 如图,将三角尺ABC、ACD摆放在一起,设BD交AC于点E,则△ABE∽
如图,将三角尺ABC、ACD摆放在一起,设BD交AC于点E,则△ABE∽
 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y= 三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?
三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?