题目内容
6.在一个不透明的袋中,装有2个红球和1个白球,这些球除颜色外其余都相同.搅均后从中随机一次摸出两个球,则两个球都是红球的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到红球的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,两次都摸到红球的有2种情况,
∴两个球都是红球的概率是$\frac{2}{6}$=$\frac{1}{3}$,
故选:C.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
17.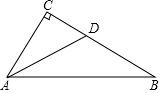 如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( )
如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( )
 如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( )
如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,若CD=2,AB=8,则△ABD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
14.一次函数y=2x-1与反比例函数y=-x-1的图象的交点的情况为( )
| A. | 只有一个交点 | B. | 有两个交点 | C. | 没有交点 | D. | 不能确定 |
11.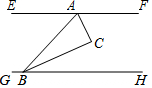 如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )
如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )
 如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )
如图,Rt△ABC的锐角顶点A、B分别在直线EF、GH上,且EF∥GH,若∠CAF=65°,则∠CBH的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
16.已知点A(x1,y1),B(x2,y2)是反比例函数y=$\frac{1}{x}$图象上的点,若x1>0>x2,则一定成立的是( )
| A. | y1>y2>0 | B. | y1>0>y2 | C. | 0>y1>y2 | D. | y2>0>y1 |
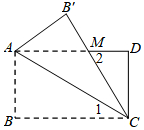 如图,将长方形纸片ABCD,沿对角线AC折叠,点B的对应点是B′,若∠1=28°,则∠2=56度.
如图,将长方形纸片ABCD,沿对角线AC折叠,点B的对应点是B′,若∠1=28°,则∠2=56度.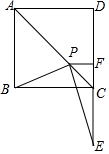 在正方形ABCD中,点P在对角线AC上,过点P作PF⊥CD于点F,作PE⊥PB交DC的延长线于点E,求证:DF=EF.
在正方形ABCD中,点P在对角线AC上,过点P作PF⊥CD于点F,作PE⊥PB交DC的延长线于点E,求证:DF=EF.



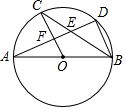 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.