题目内容
14.一次函数y=2x-1与反比例函数y=-x-1的图象的交点的情况为( )| A. | 只有一个交点 | B. | 有两个交点 | C. | 没有交点 | D. | 不能确定 |
分析 联立两函数解析式,消去x,整理成关于x的一元二次方程,利用根的判别式可求得答案.
解答 解:
联立两函数解析式可得$\left\{\begin{array}{l}{y=2x-1}\\{y=-\frac{1}{x}}\end{array}\right.$,
消去y,整理可得2x2-x+1=0,
该方程判别式为△=(-1)2=4×2×1=-7<0,
∴该一元二次方程无实数根,
∴方程组无实数解,
∴两函数图象无交点,
故选C.
点评 本题主要考查函数图象的交点问题,掌握函数图象的交点坐标即对应两函数解析式组成的方程组的解是解题的关键.

练习册系列答案
相关题目
19. 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
 如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字( )| A. | 的 | B. | 中 | C. | 国 | D. | 梦 |
6.在一个不透明的袋中,装有2个红球和1个白球,这些球除颜色外其余都相同.搅均后从中随机一次摸出两个球,则两个球都是红球的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
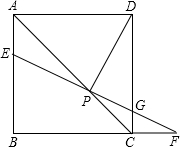 已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.
已知:如图,点P是正方形ABCD的对角线AC上一点,过点P作EF⊥DP,交AB于点E,交CD于点G,交BC的延长线于点F.